
【题目】某校数学课外兴趣小组为研究数学成绩是否与性别有关,先统计本校高二年级每个学生一学期数学成绩平均分(采用百分制),剔除平均分在30分以下的学生后,共有男生300名,女生200名,现采用分层抽样的方法,从中抽取了100名学生,按性别分为两组,并将两组学生成绩分为6组,得到如下所示频数分布表.
分数段 |
|
|
|
|
|
|
男 | 3 | 9 | 18 | 15 | 6 | 9 |
女 | 6 | 4 | 5 | 10 | 13 | 2 |
附表及公式:
| 0.100 | 0.050 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |
![]()
(1)估计男、女生各自的平均分(同一组数据用该组区间中点值作代表),从计算结果看,数学成绩与性别是否有关;
(2)规定80分以上者为优分(含80分),请你根据已知条件作出 ![]() 列联表,并判断是否有90%以上的把握认为“数学成绩与性别有关”.
列联表,并判断是否有90%以上的把握认为“数学成绩与性别有关”.
【答案】
(1)
解:男生的平均分为:
![]()
女生的平均分为:
![]()
从男、女生各自的平均分来看,并不能判断数学成绩与性别有关.
(2)
解:由频数分布表可知:在抽取的100名学生中,“男生组”中的优分有15人,“女生组”中的优分有15人,据此可得 ![]() 列联表如下:
列联表如下:
优分 | 非优分 | 合计 | |
男生 | 15 | 45 | 60 |
女生 | 15 | 25 | 40 |
合计 | 30 | 70 | 100 |
可得 ![]() ,
,
因为 ![]() ,所以没有90%以上的把握认为“数学成绩与性别有关”.
,所以没有90%以上的把握认为“数学成绩与性别有关”.
【解析】本题主要考查了独立性检验的应用,解决问题的关键是(1)根据分层比 ![]() ,男生抽取60人,女生抽取40人,利用频数分布表计算平均值,用每一段的中点计算加权平均数,(2)根据频数分布表填写
,男生抽取60人,女生抽取40人,利用频数分布表计算平均值,用每一段的中点计算加权平均数,(2)根据频数分布表填写 ![]() 列联表,根据
列联表,根据 ![]() 的计算公式,和
的计算公式,和 ![]() 比较大小,小说明没有
比较大小,小说明没有 ![]() 把握认为有关.
把握认为有关.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
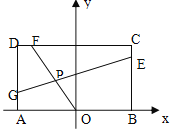
【题目】已知常数![]() ,在矩形ABCD中,
,在矩形ABCD中, ![]() ,
, ![]() ,O为AB的中点,点E、F、G分别在BC、CD、DA上移动,且
,O为AB的中点,点E、F、G分别在BC、CD、DA上移动,且![]() ,P为GE与OF的交点(如图),问是否存在两个定点,使P到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由
,P为GE与OF的交点(如图),问是否存在两个定点,使P到这两点的距离的和为定值?若存在,求出这两点的坐标及此定值;若不存在,请说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)为奇函数,当x≥0时,f(x)= ![]() .g(x)=
.g(x)= ![]() ,
,
(1)求当x<0时,函数f(x)的解析式;
(2)求g(x)的解析式,并证明g(x)的奇偶性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“ALS冰桶挑战赛”是一项社交网络上发起的筹款活动,活动规定:被邀请者要么在24小时内接受挑战,要么选择为慈善机构捐款(不接受挑战),并且不能重复参加该活动.若被邀请者接受挑战,则他需在网络上发布自己被冰水浇遍全身的视频内容,然后便可以邀请另外3个人参与这项活动.假设每个人接受挑战与不接受挑战是等可能的,且互不影响.
附: ![]()
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
(1)若某参与者接受挑战后,对其他3个人发出邀请,则这3个人中恰有2个人接受挑战的概率是多少?
(2)为了解冰桶挑战赛与受邀者的性别是否有关,某调查机构进行了随机抽样调查,调查得到如下 ![]() 列联表:
列联表:
接受挑战 | 不接受挑战 | 合计 | |
男性 | 50 | 10 | 60 |
女性 | 25 | 15 | 40 |
合计 | 75 | 25 | 100 |
根据表中数据,是否有99%的把握认为“冰桶挑战赛与受邀者的性别有关”?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义在(﹣1,+∞)内的增函数,且f(xy)=f(x)+f(y)若f(3)=1且f(a)>f(a﹣1)+2
求:
(1)f(9)的值,
(2)求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com