已知f(x)=(x3+bx2+cx+d)•ex,且f(0)=4-5b,x=1为f(x)的极值点,g(x)=(2x+2)•e-2x.
(I)若f(x)在(2,+∞)上递增,求b的取值范围;
(II)对任意x1∈[0,1],存在x2使得f(x1)=g(x2)成立,求b的取值范围.
解:(I)由f(0)=4-5b得d=4-5b,
又f′(x)=[x
3+(b+3)x
2+(c+2b)x+c+d]e
x
∵x=1为f(x)的极值点
∴f′(1)=0
得c=b-4
f(x)=[x
3+bx
2+(b-4)x+4-5b]•e
x,
f′(x)=(x+b)(x
2+3x-4)e
x≥0,?x∈(2,+∞)恒成立,
b≥-2
(II)由g′(x)=e
-2x(-4x-2)得,g(x)在
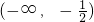
上递增,在
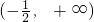
上递减.
故g(x)的值域为(-∞,e],
f′(x)=(x+b)(x
2+3x-4)e
x=(x+b)(x+4)(x-1)e
x①当-b≥1即b≤-1时,f(x)在[0,1]上递增
所以f(x)的值域为[4-5b,1-3b]
∵对任意x
1∈[0,1],存在x
2使得f(x
1)=g(x
2)成立
∴1-3b≤e
此时无解
②当0≤-b≤1即-1≤b≤0时,f(x)在[0,-b]上递增,在[-b,1]上递减
∴当x=-b时,f(x)有最大值为f(-b)=e
-b(-b
2-b+4)
∵对任意x
1∈[0,1],存在x
2使得f(x
1)=g(x
2)成立
∴e
-b(-b
2-b+4)≤e
解得不存在b
③当b>0时
f(x)在[0,1]上递减
∴f(x)的值域为[1-3b,4-5b]
∵对任意x
1∈[0,1],存在x
2使得f(x
1)=g(x
2)成立
∴4-5b≤e
解得
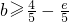
分析:(I)将x=0代入已知等式列出方程得到b,c的关系,求出f(x)的导函数,令x=1时导函数为0,得到b,c 的关系,代入f(x)的导函数,令导函数大于等于0在(2,+∞)上恒成立求出b的范围.
(II)求出g(x)的导函数,得到g(x)的单调性,求出g(x)的值域,通过对b的分类讨论求出f(x)的最大值,令f(x)的最大值属于g(x)的值域,列出不等式求出b的范围.
点评:解决已知函数的单调性求参数问题,一般求出导函数,令导函数大于等于(或小于等于0)恒成立;解决不等式恒成立问题常采用分离参数,转化为求函数的最值.

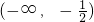 上递增,在
上递增,在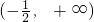 上递减.
上递减.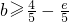


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案