练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

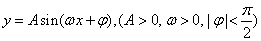    函数的最小值是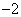，在一个周期内图象最高点与最低点横坐标差是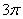，又：图象过点，

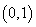    求（1）函数解析式，

    （2）函数的最大值、以及达到最大值时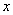的集合；

    （3）该函数图象可由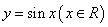的图象经过怎样的平移和伸缩得到？

    （4）当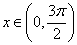时，函数的值域.

     

    【答案】

    （1）（2）2 （3）向左平移个单位，横坐标伸长到原来的3倍,纵坐标变为原来的2倍 （4）

    【解析】

    试题分析：（1）易知：A =" 2" 半周期  ∴T = 6p 即 （） 从而： 设： 令x = 0 有又：   ∴ 

    ∴所求函数解析式为 .

    （2）令，即时，有最大值2，故当时，取最大值2 .

    （3）因为，所以向左平移个单位得到，横坐标伸长到原来的3倍得到，纵坐标伸长到原来的2倍得到.

    （4）因为，所以，所以，所以

     .              

    考点：由的部分图象确定其解析式．

    点评：本题考查由的部分图象确定其解析式，确定A，ω，φ的值是关键，φ的确定是难点，属于中档题．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    经市场调查，某商场的一种商品在过去的一个月内（以30天计）销售价格f（t）（元）与时间t（天）的函数关系近似满足f(t)=100(1+
    kt
    )    （k为正常数），日销售量g（t）（件）与时间t（天）的函数关系近似满足g（t）=125-|t-25|，且第25天的销售金额为13000元．
    （Ⅰ）求k的值；
    （Ⅱ）试写出该商品的日销售金额w（t）关于时间t（1≤t≤30，t∈N）的函数关系式；
    （Ⅲ）该商品的日销售金额w（t）的最小值是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    14、数学老师给出一个函数f（x），甲、乙、丙、丁四个同学各说出了这个函数的一条性质
    甲：在（-∞，0]上函数单调递减；
    乙：在[0，+∞）上函数单调递增；
    丙：在定义域R上函数的图象关于直线x=1对称；
    丁：f（0）不是函数的最小值．
    老师说：你们四个同学中恰好有三个人说的正确． 那么，你认为
    乙
    说的是错误的．

    查看答案和解析>>

    科目：高中数学 来源：四川省自贡市2012届高三第一次诊断性考试数学理科试题 题型：022

    在实数集R上定义一种运算“*”，该运算具有性质：

    ①对任意a，b∈R，a*b＝b*a；

    ②对任意a∈R，a*0＝a；

    ③对任意a，b，c∈R，(a*b)*c＝c*(ab)＋(a*c)＋(b*c)－2c．

    则1*2＝_________；函数的最小值是_________．

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年青海省片区高三年级大联考理科数学试卷（解析版） 题型：选择题

    在实数集R中定义一种运算“﹡”，具有性质：①对任意;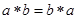

    ②对任意 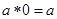 ; ③对任意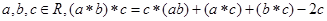

    则函数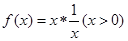的最小值是

    A.1                B.2               C.3             D.4

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在实数集中定义一种运算“”，具有性质：

    ①对任意；

    ②对任意；

    ③对任意.则     ；函数的最小值是        .

    查看答案和解析>>

    同步练习册答案