
分析 (Ⅰ)求得直线l的方程,求得与x轴的焦点坐标,则c=2,根据椭圆的离心率公式即可求得a的值,由b2=a2-c2=2,代入即可求得椭圆C的方程;
(Ⅱ)设直线l的方程代入椭圆方程根据韦达定理及向量数量积的坐标运算可知:$\frac{y_1}{{{x_1}+2}}•\frac{y_2}{{{x_2}+2}}=\frac{{{y_1}{y_2}}}{{(m{y_1}-1)(m{y_2}-1)}}=\frac{{{y_1}{y_2}}}{{{m^2}{y_1}{y_2}-m({y_1}+{y_2})+1}}=-1$,即可求得m的值,即可求得直线l的方程.
解答 解:(I)∵直线l的倾斜角为60°,
∴直线l的斜率为k=$\sqrt{3}$,
又∵直线l过点(0,-2$\sqrt{3}$),则直线l的方程为y+2$\sqrt{3}$=$\sqrt{3}$x,…(3分)
∵a>b,
∴椭圆的焦点为直线l与x轴的交点,
∴椭圆的焦点为(2,0),则c=2,
又∵e=$\frac{c}{a}$=$\frac{\sqrt{6}}{3}$,
∴a=$\sqrt{6}$,b2=a2-c2=2,
∴椭圆方程为$\frac{{x}^{2}}{6}+\frac{{y}^{2}}{2}=1$;…(5分)
(Ⅱ)设直线l的方程为x=my-3,A(x1,y1),B(x2,y2)…(6分)
联立直线与椭圆的方程$\left\{\begin{array}{l}\frac{x^2}{6}+\frac{y^2}{2}=1\\ x=my-3\end{array}\right.$,得(m2+3)y2-6my+3=0,
由韦达定理可知:${y_1}+{y_2}=\frac{6m}{{{m^2}+3}},{y_1}{y_2}=\frac{3}{{{m^2}+3}}$,…(7分)
由题意可知AF1⊥BF1,即${k_{AF}}_1•{k_{B{F_1}}}=-1$…,(8分)
∴$\frac{y_1}{{{x_1}+2}}•\frac{y_2}{{{x_2}+2}}=\frac{{{y_1}{y_2}}}{{(m{y_1}-1)(m{y_2}-1)}}=\frac{{{y_1}{y_2}}}{{{m^2}{y_1}{y_2}-m({y_1}+{y_2})+1}}=-1$,
整理得:(m2+1)y1y2-m(y1+y2)+1=0…(10分)
∴$\frac{{3({m^2}+1)}}{{{m^2}+3}}-\frac{{6{m^2}}}{{{m^2}+3}}+1=0$,解得:$m=±\sqrt{3}$…(11分)
代入△=36m2-12(m2+3)=24×3-36=36>0,…(12分)
∴直线l的方程为$x+\sqrt{3}y+3=0或x-\sqrt{3}y+3=0$.…(13分)
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,考查韦达定理,直线的斜率公式,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
 已知椭圆Cn:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=n(a>b>1,n∈N*),F1,F2是椭圆C4的焦点,A(2,$\sqrt{2}$)是椭圆C4上一点,且$\overrightarrow{A{F}_{2}}$?$\overrightarrow{{F}_{1}{F}_{2}}$=0;
已知椭圆Cn:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=n(a>b>1,n∈N*),F1,F2是椭圆C4的焦点,A(2,$\sqrt{2}$)是椭圆C4上一点,且$\overrightarrow{A{F}_{2}}$?$\overrightarrow{{F}_{1}{F}_{2}}$=0;查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3x-4y+2=0 | B. | 3x-4y+2=0,或x=2 | C. | 3x-4y+2=0,或y=2 | D. | y=2,或x=2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4 | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
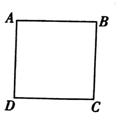 如图,正方形ABCD边长为1,从某时刻起,将线段AB,BC,CD,DA分别绕点A,B,C,D顺时针旋转相同角度α(0<α<$\frac{π}{2}$),若旋转后的四条线段所围成的封闭图形面积为$\frac{1}{2}$,则α=( )
如图,正方形ABCD边长为1,从某时刻起,将线段AB,BC,CD,DA分别绕点A,B,C,D顺时针旋转相同角度α(0<α<$\frac{π}{2}$),若旋转后的四条线段所围成的封闭图形面积为$\frac{1}{2}$,则α=( )| A. | $\frac{π}{12}$或$\frac{5π}{12}$ | B. | $\frac{π}{12}$或$\frac{π}{3}$ | C. | $\frac{π}{6}$或$\frac{5π}{12}$ | D. | $\frac{π}{6}$或$\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com