
【题目】在四棱锥![]() 中,底面
中,底面![]() 为矩形,
为矩形,![]() 平面
平面![]() 为
为![]() 的中点
的中点
(1)证明:![]() 平面
平面![]() ;
;
(2)证明:![]() 平面
平面![]() ;
;
(3)若![]() 三棱锥
三棱锥![]() 的体积为
的体积为![]() ,求点D到平面
,求点D到平面![]() 的距离.
的距离.
科目:高中数学 来源: 题型:
【题目】某商场举行促销活动,有两个摸奖箱,![]() 箱内有一个“
箱内有一个“![]() ”号球,两个“
”号球,两个“![]() ”号球,三个“
”号球,三个“![]() ”号球、四个无号球,
”号球、四个无号球,![]() 箱内有五个“
箱内有五个“![]() ”号球,五个“
”号球,五个“![]() ”号球,每次摸奖后放回,每位顾客消费额满
”号球,每次摸奖后放回,每位顾客消费额满![]() 元有一次
元有一次![]() 箱内摸奖机会,消费额满
箱内摸奖机会,消费额满![]() 元有一次
元有一次![]() 箱内摸奖机会,摸得有数字的球则中奖,“
箱内摸奖机会,摸得有数字的球则中奖,“![]() ”号球奖
”号球奖![]() 元,“
元,“![]() ”号球奖
”号球奖![]() 元,“
元,“![]() ”号球奖
”号球奖![]() 元,摸得无号球则没有奖金。
元,摸得无号球则没有奖金。
(1)经统计,顾客消费额![]() 服从正态分布
服从正态分布![]() ,某天有
,某天有![]() 位顾客,请估计消费额
位顾客,请估计消费额![]() (单位:元)在区间
(单位:元)在区间![]() 内并中奖的人数.(结果四舍五入取整数)
内并中奖的人数.(结果四舍五入取整数)
附:若![]() ,则
,则![]() ,
,![]() .
.
(2)某三位顾客各有一次![]() 箱内摸奖机会,求其中中奖人数
箱内摸奖机会,求其中中奖人数![]() 的分布列.
的分布列.
(3)某顾客消费额为![]() 元,有两种摸奖方法,
元,有两种摸奖方法,
方法一:三次![]() 箱内摸奖机会;
箱内摸奖机会;
方法二:一次![]() 箱内摸奖机会.
箱内摸奖机会.
请问:这位顾客选哪一种方法所得奖金的期望值较大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+bx2+cx-1,当x=-2时有极值,且在x=-1处的切线的斜率为-3.
(1)求函数f(x)的解析式.
(2)求函数f(x)在区间[-1,2]上的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】立德中学和树人中学各派一名学生组成一个联队参加一项智力竞赛,这个智力竞赛一共两轮,在每一轮中,两名同学各回答一次题目,已知,立德中学派出的学生每轮中答对问题的概率都是![]() ,树人中学派出的学生每轮中答对问题的概率都是
,树人中学派出的学生每轮中答对问题的概率都是![]() ;每轮中,两位同学答对与否互不影响,各论结果亦互不影响,求:
;每轮中,两位同学答对与否互不影响,各论结果亦互不影响,求:
(Ⅰ)两轮比赛后,立德中学的学生恰比树人中学的学生答对题目的个数多![]() 个的概率;
个的概率;
(Ⅱ)两轮比赛后,记![]() 为这两名同学一共答对的题目数,求随机变量
为这两名同学一共答对的题目数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左顶点为
的左顶点为![]() ,上顶点为
,上顶点为![]() ,右焦点为
,右焦点为![]() ,离心率为
,离心率为![]() ,
,![]() 的面积为
的面积为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若![]() 为
为![]() 轴上的两个动点,且
轴上的两个动点,且![]() ,直线
,直线![]() 和
和![]() 分别与椭圆
分别与椭圆![]() 交于
交于![]() 两点.
两点.
(ⅰ)求![]() 的面积最小值;
的面积最小值;
(ⅱ)证明:![]() 三点共线.
三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 与
与![]() 均为菱形,
均为菱形,![]() ,且
,且![]() .
.
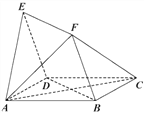
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)若![]() 为线段
为线段![]() 上的一点,且满足直线
上的一点,且满足直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的几何体中,![]() 垂直于梯形
垂直于梯形![]() 所在的平面,
所在的平面,![]() 为
为![]() 的中点,
的中点,![]() ,四边形
,四边形![]() 为矩形,线段
为矩形,线段![]() 交
交![]() 于点
于点![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 的右焦点为
的右焦点为![]() ,点
,点![]() 分别是椭圆
分别是椭圆![]() 的上、下顶点,点
的上、下顶点,点![]() 是直线
是直线![]() 上的一个动点(与
上的一个动点(与![]() 轴的交点除外),直线
轴的交点除外),直线![]() 交椭圆于另一个点
交椭圆于另一个点![]() .
.
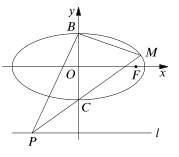
(1)当直线![]() 经过椭圆的右焦点
经过椭圆的右焦点![]() 时,求
时,求![]() 的面积;
的面积;
(2)①记直线![]() 的斜率分别为
的斜率分别为![]() ,求证:
,求证:![]() 为定值;
为定值;
②求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com