
【题目】如图,在三棱柱ABC﹣A1B1C1中,D是AC的中点,A1D⊥平面ABC,AB=BC,平面BB1D与棱A1C1交于点E.
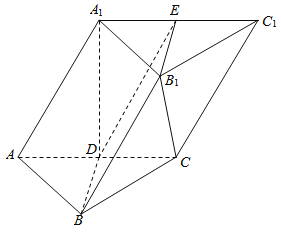
(1)求证:AC⊥A1B;
(2)求证:平面BB1D⊥平面AA1C1C;
【答案】(1)见解析;(2)见解析
【解析】
(Ⅰ)推导出A1D⊥AC,BD⊥AC,从而AC⊥平面A1BD,由此能证明AC⊥A1B.
(Ⅱ)推导出A1D⊥BD,BD⊥AC,从而BD⊥平面A1ACC1,由此能证明平面BB1D⊥平面AA1C1C.
证明:(1)因为 A1D⊥平面ABC,所以 A1D⊥AC.
因为△ABC中,AB=BC,D是AC的中点,所以 BD⊥AC.
因为 A1D∩BD=D,
所以 AC⊥平面A1BD.
所以 AC⊥A1B.
(2) 因为 A1D⊥平面ABC,
因为 BD平面ABC,所以 A1D⊥BD.
由(1)知 BD⊥AC.
因为 AC∩A1D=D,
所以 BD⊥平面A1ACC1.
因为 BD平面BB1D,
所以 平面BB1D⊥平面AA1C1C.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
【题目】已知f(x)为一次函数,g(x)为二次函数,且f[g(x)]=g[f(x)].
(1)求f(x)的解析式;
(2)若y=g(x)与x轴及y=f(x)都相切,且g(0)=![]() ,求g(x)的解析式.
,求g(x)的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,若同时满足以下条件:
,若同时满足以下条件:
①![]() 在D上单调递减或单调递增;
在D上单调递减或单调递增;
②存在区间![]() ,使
,使![]() 在
在![]() 上的值域是
上的值域是![]() ,那么称
,那么称![]() 为闭函数.
为闭函数.
(1)求闭函数![]() 符合条件②的区间
符合条件②的区间![]() ;
;
(2)判断函数![]() 是不是闭函数?若是请找出区间
是不是闭函数?若是请找出区间![]() ;若不是请说明理由;
;若不是请说明理由;
(3)若![]() 是闭函数,求实数
是闭函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=sinωx(>0)的图象向右平移 ![]() 个单位得到函数y=g(x)的图象,并且函数g(x)在区间[
个单位得到函数y=g(x)的图象,并且函数g(x)在区间[ ![]() ,
, ![]() ]上单调递增,在区间[
]上单调递增,在区间[ ![]() ]上单调递减,则实数ω的值为( )
]上单调递减,则实数ω的值为( )
A.![]()
B.![]()
C.2
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某自行车厂为共享单车公司生产新样式的单车,已知生产新样式单车的固定成本为20000元,每生产一件新样式单车需要增加投入100元.根据初步测算,自行车厂的总收益(单位:元)满足分段函数h(x),其中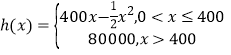 ,x是新样式单车的月产量(单位:件),利润=总收益﹣总成本.
,x是新样式单车的月产量(单位:件),利润=总收益﹣总成本.
(1)试将自行车厂的利润y元表示为月产量x的函数;
(2)当月产量为多少件时自行车厂的利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com