
 如图,x轴非负半轴平分∠AOB,∠AOx=α,动圆P截OA所得弦MN=2a,截OB所得弦SQ=2b,试求动圆圆心P的轨迹方程.
如图,x轴非负半轴平分∠AOB,∠AOx=α,动圆P截OA所得弦MN=2a,截OB所得弦SQ=2b,试求动圆圆心P的轨迹方程. 分析 建立如图所示的坐标系,由题意∠AOB=2α,利用勾股定理,确定d12-d22=b2-r2,即可求动圆圆心P的轨迹方程.
解答 解:建立如图所示的坐标系,由题意∠AOB=2α,动圆在角两边OA,OB上截得弦长分别为|MN|=2a,|QS|=2b,
设P(x,y)为轨迹上任一点,设动圆半径为r,点P到OA,OB的距离分别为|PC|=d1,|PD|=d2,
∴d12+a2=d22+b2=r2,
∴d12-d22=b2-r2,①
直线OA,OB的方程分别为OA:xsinα-ycosα=0,OB:xsinα+ycosα=0
∴d1=|xsinα-ycosα|,d2=|xsinα+ycosα|
代入①化简可得2xysin2α=a2-b2.
点评 本题考查轨迹方程,考查直接法的运用,考查学生分析解决问题的能力,属于中档题.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
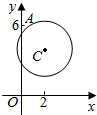 已知某市野生动物园中有猛虎出没,三位青年为抄近路返回市区(从A点出发,沿y轴负方向走直线),决定冒险穿越野生动物园,如图,设老虎出没的区域为圆C:(x-2)2+(y-4)2=$\frac{25}{4}$所含区域,三位青年从A(0,6)到O需要40min,若三位青年在老虎出没的地区逗留时间超过15min就有生命危险.问:三位青年是否有生命危险?(假设三位青年以匀速返回市区)
已知某市野生动物园中有猛虎出没,三位青年为抄近路返回市区(从A点出发,沿y轴负方向走直线),决定冒险穿越野生动物园,如图,设老虎出没的区域为圆C:(x-2)2+(y-4)2=$\frac{25}{4}$所含区域,三位青年从A(0,6)到O需要40min,若三位青年在老虎出没的地区逗留时间超过15min就有生命危险.问:三位青年是否有生命危险?(假设三位青年以匀速返回市区)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{10}$a | B. | $\frac{3\sqrt{7}}{10}$a | C. | $\frac{3\sqrt{5}}{10}$a | D. | $\frac{7}{10}$a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
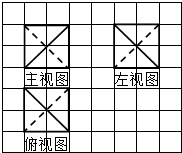
| A. | $\frac{2\sqrt{3}}{9π}$ | B. | $\frac{\sqrt{3}}{9π}$ | C. | $\frac{\sqrt{2}}{16π}$ | D. | $\frac{8\sqrt{2}}{π}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com