
【题目】已知函数![]() (其中
(其中![]() ),
),![]() .它的最小正周期为
.它的最小正周期为![]() ,
,![]() ,且
,且![]() 的最大值为2.
的最大值为2.
(1)求![]() 的解析式;
的解析式;
(2)写出函数![]() 的单调递减区间、对称轴和对称中心.
的单调递减区间、对称轴和对称中心.
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
【题目】为了弘扬民族文化,某中学举行了“我爱国学,传诵经典”考试,并从中随机抽取了60名学生的成绩(满分100分)作为样本,其中成绩不低于80分的学生被评为优秀生,得到成绩分布的频率分布直方图如图所示.

(1)若该所中学共有2000名学生,试利用样本估计全校这次考试中优秀生人数;
(2)(i)试估计这次参加考试的学生的平均成绩(同一组数据用该组区间的中点值作代表);
(ii)若在样本中,利用分层抽样的方法从成绩不低于70分的学生中随机抽取6人,再从中抽取3人赠送一套国学经典学籍,试求恰好抽中2名优秀生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,椭圆
中,椭圆![]() 的方程为
的方程为![]() (
(![]() 为参数);以原点
为参数);以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系,圆
轴正半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求椭圆![]() 的极坐标方程,及圆
的极坐标方程,及圆![]() 的直角坐标方程;
的直角坐标方程;
(2)若动点![]() 在椭圆
在椭圆![]() 上,动点
上,动点![]() 在圆
在圆![]() 上,求
上,求![]() 的最大值;
的最大值;
(3)若射线![]() 分别与椭圆
分别与椭圆![]() 交于点
交于点![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体![]() 中边长AB为2,P为正方形A1B1C1D1四边上的动点,O为底面正方形ABCD的中心,Q为正方形ABCD内一点,M,N分别为AB,BC上靠近A和C的三等分点,若线段
中边长AB为2,P为正方形A1B1C1D1四边上的动点,O为底面正方形ABCD的中心,Q为正方形ABCD内一点,M,N分别为AB,BC上靠近A和C的三等分点,若线段![]() 与OP相交且互相平分,则点Q的轨迹与线段MN形成的封闭图形的面积为____.
与OP相交且互相平分,则点Q的轨迹与线段MN形成的封闭图形的面积为____.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,圆
,圆![]() .
.
(1)若直线![]() 过点
过点![]() 且到圆心
且到圆心![]() 的距离为
的距离为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)设过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于
交于![]() 、
、![]() 两点(
两点(![]() 的斜率为负),当
的斜率为负),当![]() 时,求以线段
时,求以线段![]() 为直径的圆的方程.
为直径的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某篮球比赛采用7局4胜制,即若有一队先胜4局,则此队获胜,比赛就此结束.由于参加比赛的两队实力相当,每局比赛两队获胜的可能性均为![]() .据以往资料统计,第一局比赛组织者可获得门票收入40万元,以后每局比赛门票收入比上一局增加10万元,则组织者在此次比赛中获得的门票收入不少于390万元的概率为________.
.据以往资料统计,第一局比赛组织者可获得门票收入40万元,以后每局比赛门票收入比上一局增加10万元,则组织者在此次比赛中获得的门票收入不少于390万元的概率为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() :
:![]() ,直线
,直线![]() :
:![]() .以极点
.以极点![]() 为原点,极轴为
为原点,极轴为![]() 轴的正半轴建立平面直角坐标系.
轴的正半轴建立平面直角坐标系.
(1)求直线![]() ,
,![]() 的直角坐标方程以及曲线
的直角坐标方程以及曲线![]() 的参数方程;
的参数方程;
(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,直线
两点,直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为2的正方形,平面
是边长为2的正方形,平面![]()
![]()
![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点.
的中点.
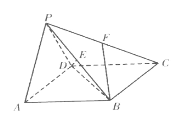
(1)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com