
【题目】已知动圆过定点![]() ,且在
,且在![]() 轴上截得的弦长为
轴上截得的弦长为![]() ,记动圆圆心的轨迹为曲线
,记动圆圆心的轨迹为曲线![]() .
.
(1)求直线![]() 与曲线
与曲线![]() 围成的区域面积;
围成的区域面积;
(2)点![]() 在直线
在直线![]() 上,点
上,点![]() ,过点
,过点![]() 作曲线
作曲线![]() 的切线
的切线![]() 、
、![]() ,切点分别为
,切点分别为![]() 、
、![]() ,证明:存在常数
,证明:存在常数![]() ,使得
,使得![]() ,并求
,并求![]() 的值.
的值.
【答案】(1)![]() ;(2)答案见解析。
;(2)答案见解析。
【解析】试题分析:
(1)根据直接法求得曲线方程为![]() ,解方程组得到直线和曲线C的交点坐标,根据定积分可求得面积.(2)设
,解方程组得到直线和曲线C的交点坐标,根据定积分可求得面积.(2)设![]() 、
、![]() ,结合题意求得切线
,结合题意求得切线![]() 的方程,根据切线方程的特点求出直线
的方程,根据切线方程的特点求出直线![]() 的方程,将直线
的方程,将直线![]() 的方程与
的方程与![]() 联立消元后得到二次方程,根据根与系数的关系求得
联立消元后得到二次方程,根据根与系数的关系求得![]() 和
和![]() 后比较可得
后比较可得![]() ,从而得到结论.
,从而得到结论.
试题解析:
(1) 设动圆圆心的坐标为![]() ,
,
由题意可得![]() ,
,
化简得![]() ,
,
故曲线![]() 的方程为
的方程为![]() .
.
由![]() ,解得
,解得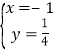 或
或![]() ,
,
所以直线![]() 与曲线
与曲线![]() 围成的区域面积为
围成的区域面积为![]() .
.
(2)设![]() 、
、![]() ,
,
则由题意得切线![]() 的方程为
的方程为![]() ,切线
,切线![]() 的方程为
的方程为![]() ,设点
,设点![]() ,
,
从而有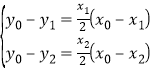 ,
,
所以可得直线AB的方程为![]()
即![]() .
.
由 消去y整理得
消去y整理得![]() ,
,
又![]() ,
,
所以![]() ,
,
所以![]() ,
,
故![]() ,
,
![]()
![]()
![]()
= ![]() ,
,
所以![]() .
.
故存在常数![]() ,使得
,使得![]() 成立.
成立.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在平面直角坐标系中,直线![]() 的参数方程为
的参数方程为 (其中t为参数),现以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(其中t为参数),现以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)写出直线l普通方程和曲线C的直角坐标方程;
(2)过点![]() 且与直线
且与直线![]() 平行的直线
平行的直线![]() 交
交![]() 于
于![]() ,
, ![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,菱形ABCD与正三角形BCE的边长均为2,且平面ABCD⊥平面BCE,![]() 平面ABCD,
平面ABCD,![]() .
.

(I)求证:![]() 平面ABCD;
平面ABCD;
(II)求证:平面ACF⊥平面BDF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某幼儿园雏鹰班的生活老师统计2018年上半年每个月的20日的昼夜温差![]() ,
,![]() 和患感冒的小朋友人数(
和患感冒的小朋友人数(![]() /人)的数据如下:
/人)的数据如下:
温差 |
|
|
|
|
|
|
患感冒人数 | 8 | 11 | 14 | 20 | 23 | 26 |
其中![]() ,
,![]() ,
,![]() .
.
(Ⅰ)请用相关系数加以说明是否可用线性回归模型拟合![]() 与
与![]() 的关系;
的关系;
(Ⅱ)建立![]() 关于
关于![]() 的回归方程(精确到
的回归方程(精确到![]() ),预测当昼夜温差升高
),预测当昼夜温差升高![]() 时患感冒的小朋友的人数会有什么变化?(人数精确到整数)
时患感冒的小朋友的人数会有什么变化?(人数精确到整数)
参考数据:![]() .参考公式:相关系数:
.参考公式:相关系数: ,回归直线方程是
,回归直线方程是![]() ,
,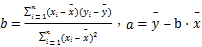 ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每当《我心永恒》这首感人唯美的歌曲回荡在我们耳边时,便会想起电影《泰坦尼克号》中一暮暮感人画面,让我们明白了什么是人类的“真、善、美”.为了推动我市旅游发展和带动全市经济,更为了向外界传递遂宁人民的“真、善、美”.我市某地将按“泰坦尼克号”原型![]() 比例重新修建.为了了解该旅游开发在大众中的熟知度,随机从本市
比例重新修建.为了了解该旅游开发在大众中的熟知度,随机从本市![]() 岁的人群中抽取了
岁的人群中抽取了![]() 人,得到各年龄段人数的频率分布直方图如图所示,现让他们回答问题“该旅游开发将在我市哪个地方建成?”,统计结果如下表所示:
人,得到各年龄段人数的频率分布直方图如图所示,现让他们回答问题“该旅游开发将在我市哪个地方建成?”,统计结果如下表所示:
组号 | 分组 | 回答正确的人数 | 回答正确的人数 占本组的频率 |
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|

(1)求出![]() 的值;
的值;
(2)从第![]() 组回答正确的人中用分层抽样的方法抽取
组回答正确的人中用分层抽样的方法抽取![]() 人,求第
人,求第![]() 组每组抽取的人数;
组每组抽取的人数;
(3)在(2)中抽取的![]() 人中随机抽取
人中随机抽取![]() 人,求所抽取的人中恰好没有年龄在
人,求所抽取的人中恰好没有年龄在![]() 段的概率.
段的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从标准质量为500g的一批洗衣粉中,随机抽查了50袋,测得的质量数据如下(单位:g):
494 498 493 494 496 492 490 490 500 499 494 495 482 485 502
493 505 485 501 491 493 500 509 512 484 509 510 494 497 498
504 498 483 510 503 497 502 498 497 500 493 499 505 493 491
497 515 503 498 518
(1)找出这组数的最值,求出极差;
(2)以![]() 为第一个分组的区间,作出这组数的频率分布表.
为第一个分组的区间,作出这组数的频率分布表.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面直角坐标系上一动点![]() 到点
到点![]() 的距离是点
的距离是点![]() 到点
到点![]() 的距离的2倍。
的距离的2倍。
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)若点![]() 与点
与点![]() 关于点
关于点![]() 对称,求
对称,求![]() ,
,![]() 两点间距离的最大值。
两点间距离的最大值。
(3)若过点![]() 的直线
的直线![]() 与点
与点![]() 的轨迹
的轨迹![]() 相交于
相交于![]() 、
、![]() 两点,
两点,![]() ,则是否存在直线
,则是否存在直线![]() ,使
,使![]() 取得最大值,若存在,求出此时
取得最大值,若存在,求出此时![]() 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,且短轴长为6.
,且短轴长为6.
(1)求椭圆的标准方程;
(2)是否存在斜率为1的直线l,使得l与曲线C相交于A,B两点,且以AB为直径的圆恰好经过原点?若存在,求出直线l的方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com