
【题目】如图,三棱柱ABC﹣A1B1C1中,侧棱与底面垂直,AB=AC=1,AA1=2,且P,Q,M分别是BB1 , CC1 , B1C1的中点,AB⊥AQ. 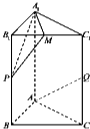
(1)求证:AB⊥AC;
(2)求证:AQ∥平面A1PM;
(3)求AQ与平面BCC1B1所成角的大小.
【答案】
(1)证明:∵A1A⊥面ABC,而AB面ABC,∴AB⊥A1A,
又∵AB⊥AQ,
∴AB⊥面ACC1A1,
又∵AC面ACC1A1,
∴AB⊥AC
(2)证明:取BC的中点G,连接AG、QG、BC1,
∵P、M分别是BB1、B1C1的中点,
∴MP∥BC1,
同理:QG∥BC1,
∴QG∥MP,
又∵M为B1C1的中点,G为BC中点,
∴A1M∥AG,
又∵QG∥MP,
∴面APQ∥面A1PM,
∴AQ∥平面A1PM
(3)解:取BC的中点G,连接AG、DG,
∵AB=AC=1,
∴AG⊥BC,
又∵AG⊥BB1,
∴AG⊥面BCC1B1,
故∠AQG为直线AQ与平面BCC1B1所成角,
在△ABC中,∠ABC=90°,AB=AC=1,则BC= ![]() 且AG=
且AG= ![]() ,
,
在Rt△AQG中,AG= ![]() ,GQ=
,GQ= ![]() =
= ![]() ,
,
则tan∠AQG= ![]() =
= ![]() ,
,
则∠AQG=30°.
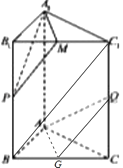
【解析】(1)由于三棱柱中侧棱与底面垂直,分析可得AB⊥A1A,又由题干条件AB⊥AQ,由线面垂直的判定定理即可得证明;(2)取BC的中点G,连接AG、QG、BC1 , 由中位线的性质可得可得MP∥BC1与QG∥BC1 , 进而可得QG∥MP,分析可得A1M∥AG,由面面平行的判定方法可得面APQ∥面A1PM,进而结合面面平行的性质可得证明;(3)取BC的中点G,连接AG、DG,分析易得AG⊥面BCC1B1 , 进而由线面角的定义可得∠AQG为直线AQ与平面BCC1B1所成角;在△ABC中分析可得BC= ![]() AG=
AG= ![]() ,进而在Rt△AQG中,计算可得AG=
,进而在Rt△AQG中,计算可得AG= ![]() ,GQ=
,GQ= ![]() =
= ![]() ,由正切的定义可得tan∠AQG=
,由正切的定义可得tan∠AQG= ![]() =
= ![]() ,计算即可得答案.
,计算即可得答案.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行,以及对空间角的异面直线所成的角的理解,了解已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则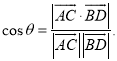 .
.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:
【题目】设 ![]() ,
, ![]() 是平面
是平面 ![]() 的一组基底,则能作为平面
的一组基底,则能作为平面 ![]() 的一组基底的是( )
的一组基底的是( )
A.![]() ﹣
﹣ ![]() ,
, ![]() ﹣
﹣ ![]()
B.![]() +2
+2 ![]() ,
, ![]() +
+ ![]()
C.2 ![]() ﹣3
﹣3 ![]() ,6
,6 ![]() ﹣4
﹣4 ![]()
D.![]() +
+ ![]() ,
, ![]() ﹣
﹣ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点(1,﹣2)和( ![]() ,0)在直线l:ax﹣y﹣1=0(a≠0)的两侧,则直线l的倾斜角的取值范围是( )
,0)在直线l:ax﹣y﹣1=0(a≠0)的两侧,则直线l的倾斜角的取值范围是( )
A.( ![]() ,
, ![]() )
)
B.( ![]() ,
, ![]() )
)
C.( ![]() ,
, ![]() )
)
D.(0, ![]() )∪(
)∪( ![]() ,π)
,π)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线y2=4x的焦点为F,过点(0,3)的直线与抛物线交于A,B两点,线段AB的垂直平分线交x轴于点D,若|AF|+|BF|=6,则点D的横坐标为 . 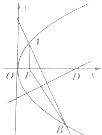
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}满足an>0,n=1,2,…,且a5a2n﹣5=22n(n≥3),则当n≥1时,log2a1+log2a3+…+log2a2n﹣1=( )
A.n(2n﹣1)
B.(n+1)2
C.n2
D.(n﹣1)2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2x﹣8,g(x)=2x2﹣4x﹣16,
(1)求不等式g(x)<0的解集;
(2)若对一切x>5,均有f(x)≥(m+2)x﹣m﹣15成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】各项均为正数的等差数列{an}前n项和为Sn , 首项a1=3,数列{bn} 为等比数列,首项b1=1,且b2S2=64,b3S3=960.
(1)求an和bn;
(2)设f(n)= ![]() (n∈N*),求f(n)最大值及相应的n的值.
(n∈N*),求f(n)最大值及相应的n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】是否存在同时满足下列两条件的直线l:l与抛物线y2=8x有两个不同的交点A和B;线段AB被直线l1:x+5y﹣5=0垂直平分.若不存在,说明理由,若存在,求出直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com