
【题目】某早餐店对一款新口味的酸奶进行了一段时间试销,定价为![]() 元/瓶.酸奶在试销售期间足量供应,每天的销售数据按照
元/瓶.酸奶在试销售期间足量供应,每天的销售数据按照![]() ,
,![]() ,
,![]() ,
,![]() 分组,得到如下频率分布直方图,以不同销量的频率估计概率.
分组,得到如下频率分布直方图,以不同销量的频率估计概率.
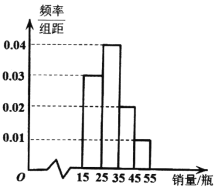
![]() 从试销售期间任选三天,求其中至少有一天的酸奶销量大于
从试销售期间任选三天,求其中至少有一天的酸奶销量大于![]() 瓶的概率;
瓶的概率;
![]() 试销结束后,这款酸奶正式上市,厂家只提供整箱批发:大箱每箱
试销结束后,这款酸奶正式上市,厂家只提供整箱批发:大箱每箱![]() 瓶,批发成本
瓶,批发成本![]() 元;小箱每箱
元;小箱每箱![]() 瓶,批发成本
瓶,批发成本![]() 元.由于酸奶保质期短,当天未卖出的只能作废.该早餐店以试销售期间的销量作为参考,决定每天仅批发一箱(计算时每个分组取中间值作为代表,比如销量为
元.由于酸奶保质期短,当天未卖出的只能作废.该早餐店以试销售期间的销量作为参考,决定每天仅批发一箱(计算时每个分组取中间值作为代表,比如销量为![]() 时看作销量为
时看作销量为![]() 瓶).
瓶).
①设早餐店批发一大箱时,当天这款酸奶的利润为随机变量![]() ,批发一小箱时,当天这款酸奶的利润为随机变量
,批发一小箱时,当天这款酸奶的利润为随机变量![]() ,求
,求![]() 和
和![]() 的分布列和数学期望;
的分布列和数学期望;
②以利润作为决策依据,该早餐店应每天批发一大箱还是一小箱?
注:销售额=销量×定价;利润=销售额-批发成本.
【答案】![]()
![]() ;
;![]() ①详见解析;②应该批发一大箱.
①详见解析;②应该批发一大箱.
【解析】
![]() 酸奶每天销量大于
酸奶每天销量大于![]() 瓶的概率为
瓶的概率为![]() ,不大于
,不大于![]() 瓶的概率为
瓶的概率为![]() ,设“试销售期间任选三天,其中至少有一天的酸奶销量大于
,设“试销售期间任选三天,其中至少有一天的酸奶销量大于![]() 瓶”为事件
瓶”为事件![]() ,则
,则![]() 表示“这三天酸奶的销量都不大于
表示“这三天酸奶的销量都不大于![]() 瓶”.利用对立事件概率公式求解即可.
瓶”.利用对立事件概率公式求解即可.
![]() ①若早餐店批发一大箱,批发成本为
①若早餐店批发一大箱,批发成本为![]() 元,依题意,销量有
元,依题意,销量有![]() ,
,![]() ,
,![]() ,
,![]() 四种情况,分别求出相应概率,列出分布列,求出
四种情况,分别求出相应概率,列出分布列,求出![]() 的数学期望,若早餐店批发一小箱,批发成本为
的数学期望,若早餐店批发一小箱,批发成本为![]() 元,依题意,销量有
元,依题意,销量有![]() ,
,![]() 两种情况,分别求出相应概率,由此求出
两种情况,分别求出相应概率,由此求出![]() 的分布列和数学期望;②根据①中的计算结果,
的分布列和数学期望;②根据①中的计算结果,![]() ,从而早餐应该批发一大箱.
,从而早餐应该批发一大箱.
解:![]() 根据图中数据,酸奶每天销量大于
根据图中数据,酸奶每天销量大于![]() 瓶的概率为
瓶的概率为![]() ,不大于
,不大于![]() 瓶的概率为
瓶的概率为![]() .
.
设“试销售期间任选三天,其中至少有一天的酸奶销量大于![]() 瓶”为事件
瓶”为事件![]() ,则
,则![]() 表示“这三天酸奶的销量都不大于
表示“这三天酸奶的销量都不大于![]() 瓶”.
瓶”.
所以![]() .
.
![]() ①若早餐店批发一大箱,批发成本为
①若早餐店批发一大箱,批发成本为![]() 元,依题意,销量有
元,依题意,销量有![]() ,
,![]() ,
,![]() ,
,![]() 四种情况.
四种情况.
当销量为![]() 瓶时,利润为
瓶时,利润为![]() 元;
元;
当销量为![]() 瓶时,利润为
瓶时,利润为![]() 元;
元;
当销量为![]() 瓶时,利润为
瓶时,利润为![]() 元;
元;
当销量为![]() 瓶时,利润为
瓶时,利润为![]() 元.
元.
随机变量![]() 的分布列为
的分布列为
|
|
|
|
|
|
|
|
|
|
所以![]() (元)
(元)
若早餐店批发一小箱,批发成本为![]() 元,依题意,销量有
元,依题意,销量有![]() ,
,![]() 两种情况.
两种情况.
当销量为![]() 瓶时,利润为
瓶时,利润为![]() 元;
元;
当销量为![]() 瓶时,利润为
瓶时,利润为![]() 元.
元.
随机变量![]() 的分布列为
的分布列为
|
|
|
|
|
|
所以![]() (元).
(元).
②根据①中的计算结果,![]() ,
,
所以早餐店应该批发一大箱.


科目:高中数学 来源: 题型:
【题目】已知a∈R,函数f(x)=(-x2+ax)ex(x∈R).
(1)当a=2时,求函数f(x)的单调区间;
(2)若函数f(x)在(-1,1)上单调递增,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】虚拟现实(![]() )技术被认为是经济发展的新增长点,某地区引进
)技术被认为是经济发展的新增长点,某地区引进![]() 技术后,
技术后,![]() 市场收入(包含软件收入和硬件收入)逐年翻一番,据统计该地区
市场收入(包含软件收入和硬件收入)逐年翻一番,据统计该地区![]() 市场收入情况如图所示,则下列说法错误的是( )
市场收入情况如图所示,则下列说法错误的是( )
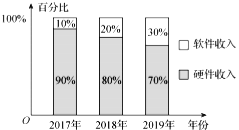
A.该地区2019年的![]() 市场总收入是2017年的4倍
市场总收入是2017年的4倍
B.该地区2019年的![]() 硬件收入比2017年和2018年的硬件收入总和还要多
硬件收入比2017年和2018年的硬件收入总和还要多
C.该地区2019年的![]() 软件收入是2018年的软件收入的3倍
软件收入是2018年的软件收入的3倍
D.该地区2019年的![]() 软件收入是2017年的软件收入的6倍
软件收入是2017年的软件收入的6倍
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图,90后从事互联网行业岗位分布条形图,则下列结论中不正确的是( )
注:90后指1990年及以后出生,80后指1980-1989年之间出生,80前指1979年及以前出生.


A.互联网行业从业人员中90后占一半以上
B.互联网行业中从事技术岗位的人数超过总人数的![]()
C.互联网行业中从事运营岗位的人数90后比80前多
D.互联网行业中从事技术岗位的人数90后比80后多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网络平台从购买该平台某课程的客户中,随机抽取了100位客户的数据,并将这100个数据按学时数,客户性别等进行统计,整理得到如表:
学时数 |
|
|
|
|
|
|
|
男性 | 18 | 12 | 9 | 9 | 6 | 4 | 2 |
女性 | 2 | 4 | 8 | 2 | 7 | 13 | 4 |
(1)根据上表估计男性客户购买该课程学时数的平均值(同一组中的数据用该组区间的中点值作代表,结果保留小数点后两位);
(2)从这100位客户中,对购买该课程学时数在20以下的女性客户按照分层抽样的方式随机抽取7人,再从这7人中随机抽取2人,求这2人购买的学时数都不低于15的概率.
(3)将购买该课程达到25学时及以上者视为“十分爱好该课程者”,25学时以下者视,为“非十分爱好该课程者”.请根据已知条件完成以下![]() 列联表,并判断是否有99.9%的把握认为“十分爱好该课程者”与性别有关?
列联表,并判断是否有99.9%的把握认为“十分爱好该课程者”与性别有关?
非十分爱好该课程者 | 十分爱好该课程者 | 合计 | |
男性 | |||
女性 | |||
合计 | 100 |
附:![]() ,
,![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】很多关于整数规律的猜想都通俗易懂,吸引了大量的数学家和数学爱好者,有些猜想已经被数学家证明,如“费马大定理”,但大多猜想还未被证明,如“哥德巴赫猜想”、“角谷猜想”.“角谷猜想”的内容是:对于每一个正整数,如果它是奇数,则将它乘以![]() 再加1;如果它是偶数,则将它除以
再加1;如果它是偶数,则将它除以![]() ;如此循环,最终都能够得到
;如此循环,最终都能够得到![]() .下图为研究“角谷猜想”的一个程序框图.若输入
.下图为研究“角谷猜想”的一个程序框图.若输入![]() 的值为
的值为![]() ,则输出i的值为( )
,则输出i的值为( )
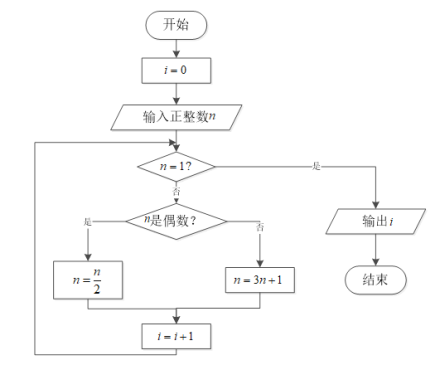
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com