
【题目】已知![]()
(1)若a=1,且f(x)≥m在(0,+∞)恒成立,求实数m的取值范围;
(2)当![]() 时,若x=0不是f(x)的极值点,求实数a的取值.
时,若x=0不是f(x)的极值点,求实数a的取值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)由![]() 在
在![]() 上恒成立,即先求
上恒成立,即先求![]() 在
在![]() 上的最小值,利用导函数判断
上的最小值,利用导函数判断![]() 的单调性,即可求得
的单调性,即可求得![]() 的范围,进而求解;
的范围,进而求解;
(2)先求导可得![]() ,将
,将![]() 代入
代入![]() ,若
,若![]() 不是
不是![]() 的极值点,即使得
的极值点,即使得![]() 是
是![]() 的非变号零点,利用导函数分别讨论当
的非变号零点,利用导函数分别讨论当![]() 与
与![]() 时
时![]() 与0的关系,进而求解.
与0的关系,进而求解.
解:(1)由题,当![]() 时,
时,![]() ,
,
所以![]() ,
,
设![]() ,
,
所以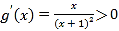 恒成立,
恒成立,
所以![]() 在
在![]() 上为增函数,
上为增函数,
所以![]() ,
,
又![]() ,
,
所以![]() 恒成立,所以
恒成立,所以![]() 在
在![]() 上为增函数,
上为增函数,
所以![]() ,所以
,所以![]()
(2)![]() ,
,
令![]() ,则
,则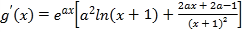 ,
,
设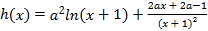 ,
,
则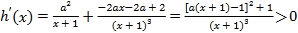 ,
,
所以![]() 在
在![]() 上递增,且
上递增,且![]() ,
,
①当![]() 时,
时,![]() ,
,
所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
即当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,
上递增,
所以![]() ,
,
所以![]() 在
在![]() 上递增,
上递增,
所以![]() 不是
不是![]() 的极值点,
的极值点,
所以![]() 时,满足条件;
时,满足条件;
②当![]() 时,
时,![]() ,
,
又因为![]() 在
在![]() 上递增,
上递增,
所以![]() ,使得
,使得![]() ,
,
所以当![]() 时,
时,![]() ,即
,即![]() ,
,
所以![]() 在
在![]() 上递增,
上递增,
又![]() ,
,
所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以![]() 是
是![]() 的极小值点,不合题意,
的极小值点,不合题意,
综上,![]()


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,过点
,过点![]() ,且该椭圆的短轴端点与两焦点
,且该椭圆的短轴端点与两焦点![]() ,
,![]() 的张角为直角.
的张角为直角.
(1)求椭圆E的方程;
(2)过点![]() 且斜率大于0的直线
且斜率大于0的直线![]() 与椭圆E相交于点P,Q,直线AP,AQ与y轴相交于M,N两点,求
与椭圆E相交于点P,Q,直线AP,AQ与y轴相交于M,N两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国是茶的故乡,也是茶文化的发源地.中国茶的发现和利用已有四千七百多年的历史,且长盛不衰,传遍全球.为了弘扬中国茶文化,某酒店推出特色茶食品“金萱排骨茶”,为了解每壶“金萱排骨茶”中所放茶叶量![]() 克与食客的满意率
克与食客的满意率![]() 的关系,通过试验调查研究,发现可选择函数模型
的关系,通过试验调查研究,发现可选择函数模型![]() 来拟合
来拟合![]() 与
与![]() 的关系,根据以下数据:
的关系,根据以下数据:
茶叶量 | 1 | 2 | 3 | 4 | 5 |
| 4.34 | 4.36 | 4.44 | 4.45 | 4.51 |
可求得y关于x的回归方程为( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() )上的两个动点
)上的两个动点![]() 和
和![]() ,焦点为F.线段AB的中点为
,焦点为F.线段AB的中点为![]() ,且A,B两点到抛物线的焦点F的距离之和为8.
,且A,B两点到抛物线的焦点F的距离之和为8.
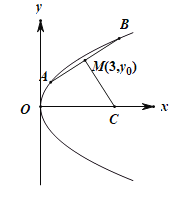
(1)求抛物线的标准方程;
(2)若线段AB的垂直平分线与x轴交于点C,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知双曲线![]() 的右焦点为F,点A,B分别在C的两条渐近线上,
的右焦点为F,点A,B分别在C的两条渐近线上,![]() 轴,
轴,![]() ,
,![]() (O为坐标原点).
(O为坐标原点).
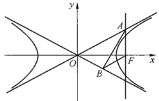
(1)求双曲线C的方程;
(2)过C上一点![]() 的直线
的直线![]() 与直线AF相交于点M,与直线
与直线AF相交于点M,与直线![]() 相交于点N.证明:当点P在C上移动时,
相交于点N.证明:当点P在C上移动时,![]() 恒为定值,并求此定值.
恒为定值,并求此定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com