
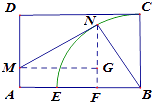
����Ŀ����ͼ��ij����С����һ���������й㳡��AB=20�ף��㳡��һ���ǰ뾶Ϊ16������BCE�̻�����Ϊ��ʹС�������ܹ����õ��ڹ㳡���з��ɣ��־����ڹ㳡�ϰ������������Σ�����һ���Ǵ�Խ�㳡��˫�˿���ֱ����MN�����Ȳ��ƣ�����M���߶�AD�ϣ�����������CE���У���һ��Ϊ���˻�����������CN�����Ȳ��ƣ��ڷţ���֪˫�˿���ֱ���ε����ÿ��Ϊ2aԪ�����˻����ε����ÿ��ΪaԪ������ǡ�NBE=�ȣ������ΪWԪ�� 
��1���Խ�W��ʾΪ�ȵĺ���W���ȣ�����д��cos�ȵ�ȡֵ��Χ��
��2�����ѡȡ��M��λ�ã���ʹ�����W��С��
���𰸡�
��1���⣺��N��AB�Ĵ��ߣ�����ΪF����M��NF�Ĵ��ߣ�����ΪG��
��Rt��BNF�У�BF=16cos�ȣ���MG=20��16cos��
��Rt��MNG�� ![]() ��
��
�������� ![]() ��
��
��ˣ� ![]() ��
�� ![]()
��2���⣺ ![]()
��W�䣨�ȣ�=0�� ![]() ����Ϊ
����Ϊ ![]() ������
������ ![]() ��
��
����Ǧ�1���� ![]() ��
�� ![]()
�� ![]() ʱ��W�����ȣ���0��W���ȣ������ݼ���
ʱ��W�����ȣ���0��W���ȣ������ݼ���
�� ![]() ʱ��W�����ȣ���0��W���ȣ�����������
ʱ��W�����ȣ���0��W���ȣ�����������
���Ե� ![]() �������W��С����СֵΪ
�������W��С����СֵΪ ![]() ��
��
��ʱ ![]() ��
�� ![]() ��
�� ![]() ��
��
��˵� ![]() ��ʱ����ʹ�������С
��ʱ����ʹ�������С
����������1����N��AB�Ĵ��ߣ�����ΪF����M��NF�Ĵ��ߣ�����ΪG������ֱ�������Σ�ͨ����ֱ�������Ρ����ɶ����ͻ�����ʽ���н�𣻣�2������1���еĺ�����ϵ���б��εõ� ![]() ��W�䣨�ȣ�=0��
��W�䣨�ȣ�=0�� ![]() ����Ϊ
����Ϊ ![]() ������
������ ![]() ��Ȼ���Ϧȵ�ȡֵ��Χ���з������ۣ��������Ǻ����ĵ����Խ��н��
��Ȼ���Ϧȵ�ȡֵ��Χ���з������ۣ��������Ǻ����ĵ����Խ��н��
�����㾫�����������Ǻ�������ֵ����Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪����![]() ����
����![]() ʱ��ȡ����СֵΪ
ʱ��ȡ����СֵΪ![]() ����
����![]() ʱ��ȡ�����ֵΪ
ʱ��ȡ�����ֵΪ![]() ����
����![]() ��
��![]() ��
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��l����ֱ��2x+y-5=0��x-2y=0�Ľ���P��
��1����ֱ��lƽ����ֱ��l1��4x-y+1=0����l�ķ��̣�
��2����ֱ��l��ֱ��ֱ��l1��4x-y+1=0����l�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ҵ2017��Ĵ�����Ϊ500��Ԫ�����豸�ϻ���ԭ����ҵ���������������½��������ܽ��м������죬Ԥ���2018����ÿ�����һ�괿�������20��Ԫ��2018�������ҵһ����Ͷ���ʽ�600��Ԫ���м������죬Ԥ����δ�۳����������ʽ������£���![]() �꣨��2018��Ϊ��һ�꣩������Ϊ
�꣨��2018��Ϊ��һ�꣩������Ϊ![]() ��Ԫ��
��Ԫ��![]() Ϊ��������.
��������.
��1����ӽ������ǰ![]() �꣬������ҵ�����м���������ۼ�������Ϊ
�꣬������ҵ�����м���������ۼ�������Ϊ![]() ��Ԫ�����м����������ۼƴ�����Ϊ
��Ԫ�����м����������ۼƴ�����Ϊ![]() ��Ԫ����۳����������ʽ𣩣���
��Ԫ����۳����������ʽ𣩣���![]() ��
��![]() �ı���ʽ��
�ı���ʽ��
��2��������Ԥ�⣬��2018�������ҵ���پ��������꣬���м����������ۼ����������м���������ۼƴ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾�ƻ�����2̨���������ֻ���ʹ���������̭.������һ����������ڹ�������ʱ�����Զ�������������Ϊ������ÿ��200Ԫ.�ڻ���ʹ���ڼ䣬������������ٹ�����ÿ��500Ԫ.��������ڹ������ʱӦͬʱ�������������Ϊ���Ѽ���������100̨���ֻ���������ʹ�����ڸ������������������������״ͼ��

����100̨���������������������Ƶ�ʴ���1̨������������������������ĸ��ʣ���![]() ��ʾ2̨���������ڹ�������������������
��ʾ2̨���������ڹ�������������������![]() ��ʾ����2̨������ͬʱ��������������.
��ʾ����2̨������ͬʱ��������������.
��������![]() �ķֲ��У�
�ķֲ��У�
��������Ҫ��![]() ��ȷ��
��ȷ��![]() ����Сֵ��
����Сֵ��
�������Թ����������������õ�����ֵΪ�������ݣ���![]() ��
��![]() ֮��ѡ��һ��Ӧѡ���ĸ���
֮��ѡ��һ��Ӧѡ���ĸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڹ������������һ����Ϸ��Ŀ����������װ��3�������2��������������װ��1�������2��������Щ�����ɫ����ȫ��ͬ��ÿ����Ϸ��������������������������2�����������İ�������2���������ÿ����Ϸ��������Ż�ԭ�䣩
��1����һ����Ϸ�У���������3������ĸ��ʣ�����ĸ��ʣ�
��2����������Ϸ�У��ǻ���ΪX������X�ķֲ��У�����X����ѧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У�ֱ��
�У�ֱ��![]() �IJ���������
�IJ��������� ��
��![]() ����������
Ϊ����������![]() Ϊ���㣬
Ϊ���㣬 ![]() ���������Ϊ���ᣬ����������ϵ������
���������Ϊ���ᣬ����������ϵ������![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() ����ֱ��
����ֱ��![]() ������
������![]() ����
����![]() ����.
����.
������ֱ��![]() ����ͨ���̼�����
����ͨ���̼�����![]() ��ֱ�����귽�̣�
��ֱ�����귽�̣�
����ֱ��![]() ��
��![]() ��Ľ����Ϊ
��Ľ����Ϊ![]() ����
����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����A��0��1����б��Ϊk��ֱ��l��ԲC����x��2��2+��y��3��2=1���ڵ�M��N���㣮
��1����k��ȡֵ��Χ��
��2���� ![]()
![]() =12������OΪ����ԭ�㣬��|MN|��
=12������OΪ����ԭ�㣬��|MN|��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��R��i��������λ������p���ڸ�ƽ���ڣ�����z1=a+ ![]() ��Ӧ�ĵ�λ�ڵڶ����ޣ�����q������z2=a��i��ģ����2����p��q�������⣬��ʵ��a��ֵ���ڣ� ��
��Ӧ�ĵ�λ�ڵڶ����ޣ�����q������z2=a��i��ģ����2����p��q�������⣬��ʵ��a��ֵ���ڣ� ��
A.��1��1
B.![]() ��
�� ![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com