
| A. | 1≤a<2 | B. | 0≤a≤1 | C. | 1≤a≤2 | D. | 2≤a≤3 |
分析 由指数与对数函数的性质作函数f(x)=$\left\{\begin{array}{l}{{2}^{x},x<1}\\{lo{g}_{3}x+1,x≥1}\end{array}\right.$的图象,从而利用数形结合求解即可.
解答 解:作函数f(x)=$\left\{\begin{array}{l}{{2}^{x},x<1}\\{lo{g}_{3}x+1,x≥1}\end{array}\right.$的图象如下,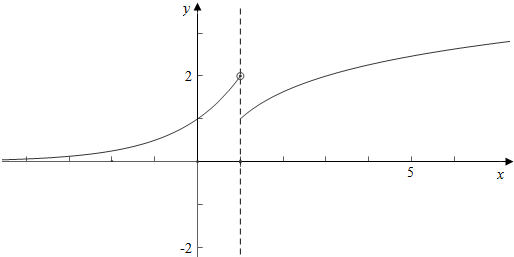
21=2,log31+1=1;
结合图象可知,
若方程f(x)=a有两个不相等的实数解,
则1≤a<2,
故选A.
点评 本题考查了分段函数的应用及数形结合的思想应用,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥S-ABCD中,SA=SB,底面ABCD是菱形,且∠ABC=60°,点E、F分别是AB、SD的中点.
如图,在四棱锥S-ABCD中,SA=SB,底面ABCD是菱形,且∠ABC=60°,点E、F分别是AB、SD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com