
【题目】已知集合A={x|x2﹣1=0},B={x|x2﹣2ax+b=0},若A∪B=A,求实数a,b满足的条件.
【答案】解:集合A={x|x2﹣1=0}={1,﹣1},
∵A∪B=A,∴BA,∴集合B有4中情况:
①B=,②B={1,﹣1},③B={﹣1},④B={1}.
以下对4中情况逐一解答:
①B=,说明B中的方程无解,即△<0,经化简得a2<b;
②B={1,﹣1},说明B中的方程有两个不同的解分别是1,﹣1,故△>0,即a2>b,
且满足 ![]() ,∴
,∴ ![]() ;
;
③B={﹣1},说明B中的方程有两个相同的解,均为﹣1,故△=0,即a2=b,
且满足1+2a+b=0,∴ ![]() ;
;
④B={1},说明B中的方程有两个相同的解,均为1,故△=0,即a2=b,
且满足1﹣2a+b=0,∴ ![]() ;
;
综上①②③④可得:a2<b或 ![]() 或
或 ![]() 或
或 ![]() .
.
【解析】根据题意可得出集合B有4中情况,逐一分情况讨论并结合利一元二次方程根的情况讨论△进而得出不同情况下a的取值范围,最后把这几种情况并起来即可的到a,b的值。
【考点精析】根据题目的已知条件,利用集合的并集运算的相关知识可以得到问题的答案,需要掌握并集的性质:(1)A![]() A∪B,B
A∪B,B![]() A∪B,A∪A=A,A∪
A∪B,A∪A=A,A∪![]() =A,A∪B=B∪A;(2)若A∪B=B,则A
=A,A∪B=B∪A;(2)若A∪B=B,则A![]() B,反之也成立.
B,反之也成立.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是直角梯形,AD⊥AB,AB∥DC,PA⊥底面ABCD,点E为棱PC的中点.AD=DC=AP=2AB=2. 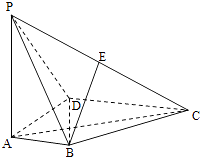
(1)证明:BE⊥平面PDC;
(2)若F为棱PC上一点,满足BF⊥AC,求二面角F﹣AD﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,设角A,B,C的对边分别为a,b,c,向量 ![]() =(cosA,sinA),
=(cosA,sinA), ![]() =(
=( ![]() ﹣sinA,cosA),若
﹣sinA,cosA),若 ![]()
![]() =1.
=1.
(1)求角A的大小;
(2)若b=4 ![]() ,且c=
,且c= ![]() a,求△ABC的面积.
a,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)的定义域为D,若满足①f(x)在D内是单调函数,②存在[a,b]D,使f(x)在[a,b]上的值域为[a,b],那么y=f(x)叫做闭函数,现有f(x)= ![]() +k是闭函数,那么k的取值范围是
+k是闭函数,那么k的取值范围是
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产一种机器的固定成本为5000元,且每生产100部,需要加大投入2500元.对销售市场进行调查后得知,市场对此产品的需求量为每年500部,已知销售收入函数为 ![]() ,其中x是产品售出的数量0≤x≤500.
,其中x是产品售出的数量0≤x≤500.
(1)若为x年产量,y表示利润,求y=f(x)的解析式
(2)当年产量为何值时,工厂的年利润最大?其最大值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法不正确的是( )
A.“φ= ![]() ”是“函数y=sin(2x+?)为偶函数”的充要条件
”是“函数y=sin(2x+?)为偶函数”的充要条件
B.若“p且q”为假,则p,q至少有一个是假命题
C.命题“?x0∈R,x02﹣x0﹣1<0”的否定是“?x∈R,x2﹣x﹣1≥0”
D.当a<0时,幂函数y=xa在(0,+∞)上是单调递减
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com