
【题目】2018年高考成绩揭晓,某高中再创辉煌,考后学校对于单科成绩逐个进行分析:现对甲、乙两个文科班的数学成绩进行分析,规定:大于等于135分为优秀,135分以下为非优秀,成绩统计后,得到如下的![]() 列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为![]() .
.
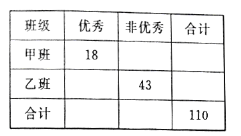
(1)请完成上面的列联表;
(2)请问:是否有75%的把握认为“数学成绩与所在的班级有关系”?
(3)用分层抽样的方法从甲、乙两个文科班的数学成绩优秀的学生中抽取5名学生进行调研,然后再从这5名学生中随机抽取2名学生进行谈话,求抽到的2名学生中至少有1名乙班学生的概率.
参考公式:![]() (其中
(其中![]() )
)
参考数据:

【答案】(1)见解析(2)有(3)![]()
【解析】分析:⑴利用已知条件直接填写联列表即可
⑵求出![]() ,即可判断结果
,即可判断结果
⑶从甲班成绩优秀的学生中抽取![]() 名,分别记为
名,分别记为![]() ,从乙班成绩优秀的学生中抽取
,从乙班成绩优秀的学生中抽取![]() 名,分别记为
名,分别记为![]() ,列出所有基本事件,设“抽到的
,列出所有基本事件,设“抽到的![]() 名学生中至少有
名学生中至少有![]() 名乙班学生”为事件
名乙班学生”为事件![]() ,求出事件
,求出事件![]() 包含的基本事件个数,然后求解概率
包含的基本事件个数,然后求解概率
详解:(1)
班级 | 优秀 | 非优秀 | 合计 |
甲班 | 37 | 55 | |
乙班 | 12 | 55 | |
合计 | 30 | 80 |
(2)由题意得![]()
所以有75%的把握认为“数学成绩与所在的班级有关系”
(3)因为甲、乙两个班数学成绩优秀的学生人数的比例为![]() ,所以从甲班成绩优秀的学生中抽取3名,
,所以从甲班成绩优秀的学生中抽取3名,
分别记为![]() ,从乙班成绩优秀的学生中抽取2名,分别记为
,从乙班成绩优秀的学生中抽取2名,分别记为![]() ,
,
则从抽取的5名学生中随机抽取2名学生的所有基本事件有![]() ,
,![]() ,共10个
,共10个
设“抽到的2名学生中至少有1名乙班学生”为事件![]() ,则事件
,则事件![]() 包含的基本事件有
包含的基本事件有![]()
![]() ,共7个,
,共7个,
所以![]() ,
,
即抽到的2名学生中至少有1名乙班学生的概率是![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]()
(1)求圆![]() 关于直线
关于直线![]() 对称的圆
对称的圆![]() 的标准方程;
的标准方程;
(2)过点![]() 的直线
的直线![]() 被圆
被圆![]() 截得的弦长为8,求直线
截得的弦长为8,求直线![]() 的方程;
的方程;
(3)当![]() 取何值时,直线
取何值时,直线![]() 与圆
与圆![]() 相交的弦长最短,并求出最短弦长.
相交的弦长最短,并求出最短弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 对一切实数
对一切实数![]() 都有
都有![]() 成立,且
成立,且![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 的解析式,并用定义法证明
的解析式,并用定义法证明![]() 在
在![]() 单调递增;
单调递增;
(3)已知![]() ,设P:
,设P:![]() ,不等式
,不等式![]() 恒成立,Q:
恒成立,Q:![]() 时,
时,![]() 是单调函数。如果满足P成立的
是单调函数。如果满足P成立的![]() 的集合记为A,满足Q成立的
的集合记为A,满足Q成立的![]() 集合记为B,求
集合记为B,求![]() (R为全集)。
(R为全集)。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂要制造A种电子装置45台,B种电子装置55台,需用薄钢板给每台装置配一个外壳,已知薄钢板的面积有两种规格:甲种薄钢板每张面积2m2,可做A、B的外壳分别为3个和5个,乙种薄钢板每张面积3m2,可做A、B的外壳分别为6个和6个,求两种薄钢板各用多少张,才能使总的面积最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若对任意实数![]() 都有函数
都有函数![]() 的图象与直线
的图象与直线![]() 相切,则称函数
相切,则称函数![]() 为“恒切函数”,设函数
为“恒切函数”,设函数![]() ,其中
,其中![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)已知函数![]() 为“恒切函数”,
为“恒切函数”,
①求实数![]() 的取值范围;
的取值范围;
②当![]() 取最大值时,若函数
取最大值时,若函数![]() 也为“恒切函数”,求证:
也为“恒切函数”,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com