
【题目】某市政府为了引导居民合理用水,决定全面实施阶梯水价,阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价:若用水量不超过12吨时,按4元/吨计算水费;若用水量超过12吨且不超过14吨时,超过12吨部分按6.60元/吨计算水费;若用水量超过14吨时,超过14吨部分按7.80元/吨计算水费.为了了解全市居民月用水量的分布情况,通过抽样,获得了100户居民的月用水量(单位:吨),将数据按照[0,2],(2,4],…,(14,16]分成8组,制成了如图1所示的频率分布直方图. 
(Ⅰ)假设用抽到的100户居民月用水量作为样本估计全市的居民用水情况.
( i)现从全市居民中依次随机抽取5户,求这5户居民恰好3户居民的月用水用量都超过12吨的概率;
(ⅱ)试估计全市居民用水价格的期望(精确到0.01);
(Ⅱ)如图2是该市居民李某2016年1~6月份的月用水费y(元)与月份x的散点图,其拟合的线性回归方程是 ![]() .若李某2016年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
.若李某2016年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
【答案】解:(Ⅰ)( i)由题意,从全市居民中依次随机抽取5户,每户居民月用水量超过12吨的概率为 ![]() ,因此这5户居民恰好3户居民的月用水用量都这超过12吨的概率为
,因此这5户居民恰好3户居民的月用水用量都这超过12吨的概率为 ![]() . ( ii)由题设条件及月均用水量的频率分布直方图,可得居民每月的水费数据分组与概率分布表如下:
. ( ii)由题设条件及月均用水量的频率分布直方图,可得居民每月的水费数据分组与概率分布表如下:
月用水量x(吨) | (0,12] | (12,14] | (14,16] |
价格X(元/吨) | 4 | 4.20 | 4.60 |
概率P | 0.9 | 0.06 | 0.04 |
所以全市居民用水价格的期望E(X)=4×0.9+4.2×0.06+4.6×0.04≈4.04吨
(Ⅱ)设李某2016年1~6月份的月用水费y(元)与月份x的对应点为(xi , yi)(i=1,2,3,4,5,6),
它们的平均值分别为 ![]() ,
, ![]() ,则
,则 ![]() ,又点
,又点 ![]() 在直线
在直线 ![]() 上,所以
上,所以 ![]() ,因此y1+y2+…+y6=240,所以7月份的水费为294.6﹣240=54.6元.
,因此y1+y2+…+y6=240,所以7月份的水费为294.6﹣240=54.6元.
设居民月用水量为t吨,相应的水费为f(t)元,则f(t)=  ,
,
t=13,f(t)=6.6×13﹣31.2=54.6,
∴李某7月份的用水吨数约为13吨
【解析】(Ⅰ)( i)由题意,从全市居民中依次随机抽取5户,每户居民月用水量超过12吨的概率为 ![]() ,即可求这5户居民恰好3户居民的月用水用量都超过12吨的概率;(ⅱ)由题设条件及月均用水量的频率分布直方图,可得居民每月的水费数据分组与概率分布表,即可估计全市居民用水价格的期望(精确到0.01);(Ⅱ)求出7月份的水费为294.6﹣240=54.6元.居民月用水量为t吨,相应的水费为f(t)元,即可得出结论.
,即可求这5户居民恰好3户居民的月用水用量都超过12吨的概率;(ⅱ)由题设条件及月均用水量的频率分布直方图,可得居民每月的水费数据分组与概率分布表,即可估计全市居民用水价格的期望(精确到0.01);(Ⅱ)求出7月份的水费为294.6﹣240=54.6元.居民月用水量为t吨,相应的水费为f(t)元,即可得出结论.


科目:高中数学 来源: 题型:
【题目】将函数f(x)=2cos2x的图象向右平移 ![]() 个单位后得到函数g(x)的图象,若函数g(x)在区间[0,
个单位后得到函数g(x)的图象,若函数g(x)在区间[0, ![]() ]和[2a,
]和[2a, ![]() ]上均单调递增,则实数a的取值范围是( )
]上均单调递增,则实数a的取值范围是( )
A.[ ![]() ,
, ![]() ]
]
B.[ ![]() ,
, ![]() ]
]
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在道路边安装路灯,路面![]() 宽
宽![]() ,灯柱
,灯柱![]() 高14
高14![]() ,灯杆
,灯杆![]() 与地面所成角为30°.路灯采用锥形灯罩,灯罩轴线
与地面所成角为30°.路灯采用锥形灯罩,灯罩轴线![]() 与灯杆
与灯杆![]() 垂直,轴线
垂直,轴线![]() ,灯杆
,灯杆![]() 都在灯柱
都在灯柱![]() 和路面宽线
和路面宽线![]() 确定的平面内.
确定的平面内.

(1)当灯杆![]() 长度为多少时,灯罩轴线
长度为多少时,灯罩轴线![]() 正好通过路面
正好通过路面![]() 的中线?
的中线?
(2)如果灯罩轴线AC正好通过路面![]() 的中线,此时有一高2.5
的中线,此时有一高2.5 ![]() 的警示牌直立在
的警示牌直立在![]() 处,求警示牌在该路灯灯光下的影子长度.
处,求警示牌在该路灯灯光下的影子长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某制造商![]() 月生产了一批乒乓球,随机抽样
月生产了一批乒乓球,随机抽样![]() 个进行检查,测得每个球的直径(单位:mm),将数据分组如下表
个进行检查,测得每个球的直径(单位:mm),将数据分组如下表
分组 | 频数 | 频率 |
| 10 | |
| 20 | |
| 50 | |
| 20 | |
合计 | 100 |

(1)请在上表中补充完成频率分布表(结果保留两位小数),并在上图中画出频率分布直方图;
(2)统计方法中,同一组数据常用该组区间的中点值(例如区间![]() 的中点值是
的中点值是![]() )作为代表.据此估计这批乒乓球直径的平均值(结果保留两位小数).
)作为代表.据此估计这批乒乓球直径的平均值(结果保留两位小数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且B=60°,c=4.
(Ⅰ)若b=6,求角C的正弦值及△ABC的面积;
(Ⅱ)若D,E在线段BC上,且BD=DE=EC, ![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=e2x(ax2+2x﹣1),a∈R.
(Ⅰ)当a=4时,求证:过点P(1,0)有三条直线与曲线y=f(x)相切;
(Ⅱ)当x≤0时,f(x)+1≥0,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出n的值为( ) (参考数据: ![]() ≈1.732,sin15°≈0.2588,sin7.5°≈0.1305)
≈1.732,sin15°≈0.2588,sin7.5°≈0.1305)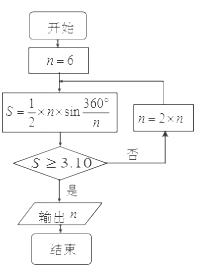
A.12
B.24
C.36
D.48
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos2A﹣3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面积S=5![]() ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com