分析:(1)设第n个等边三角形的边长为a
n,利用顶点B
n在第n个等边三角形的在抛物线上,结合B
n的纵坐标为
=an.建立等式化简得
a1+a2+…+an=+,然后再写一式,两式相减得(a
n-a
n-1-1)(a
n+a
n-1)=0,由于a
n+a
n-1≠0,所以a
n-a
n-1=1.从而可求a
n的通项公式;
(2)由已知条件可知
cn=,又因为
=<=(-),再求和利用放缩法求证即可.
解答:解:(1)设第n个等边三角形的边长为a
n.则第n个等边三角形的在抛物线上的顶点B
n的坐标为
a1+a2+…+an-1+,
).
再从第n个等边三角形上,我们可得B
n的纵坐标为
=an.
从而有
an=,
即有
=a1+a2+…+an-1+.
由此可得
a1+a2+…+an=+①
以及
a1+a2+…+an-1=+②
①-②即得
an=(an-an-1)+(an-an-1)(an+an-1).
变形可得(a
n-a
n-1-1)(a
n+a
n-1)=0.
由于a
n+a
n-1≠0,所以a
n-a
n-1=1.
在①式中取n=1,可得
a1=,而a
1≠0,故a
1=1.所以a
n=n
(2)由已知条件可知
cn=,
又因为
=<=(-)所以
+++…+<1+(-+-+…+-)<
1+-<
点评:本题主要考查数列的通项及放缩法求证不等式,同时应注意裂项求和法的应用.



 上从左向右依次取点列{Bk},k=1,2,…,使△Ak-1BkAk(k=1,2,…)都是等边三角形,其中A是坐标原点,则第2011个等边三角形的边长是 .
上从左向右依次取点列{Bk},k=1,2,…,使△Ak-1BkAk(k=1,2,…)都是等边三角形,其中A是坐标原点,则第2011个等边三角形的边长是 . 上从左向右依次取点列Bk,k=1,2,…,使△Ak-1BkAk(k=1,2,…)都是等边三角形,其中A是坐标原点,设第n个等边三角形的边长为an.
上从左向右依次取点列Bk,k=1,2,…,使△Ak-1BkAk(k=1,2,…)都是等边三角形,其中A是坐标原点,设第n个等边三角形的边长为an.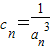 ,求证:
,求证: .
. 上从左向右依次取点列{Bk},k=1,2,…,使△Ak﹣1BkAk(k=1,2,…)都是等边三角形,其中A0是坐标原点,则第2011个等边三角形的边长是( )。
上从左向右依次取点列{Bk},k=1,2,…,使△Ak﹣1BkAk(k=1,2,…)都是等边三角形,其中A0是坐标原点,则第2011个等边三角形的边长是( )。