
【题目】如图,圆锥PO中,AB是圆O的直径,且AB=4,C是底面圆O上一点,且AC=2![]() ,点D为半径OB的中点,连接PD.
,点D为半径OB的中点,连接PD.
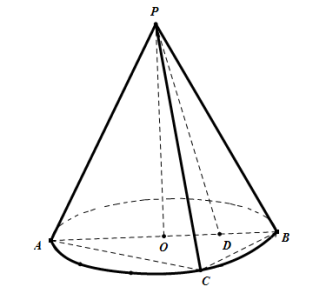
(1)求证:PC在平面APB内的射影是PD;
(2)若PA=4,求底面圆心O到平面PBC的距离.
科目:高中数学 来源: 题型:
【题目】如图,已知三棱锥P-ABC中,PA平面ABC,ABAC,且PA=l,AB=AC=2,点D满足![]() ,
,![]() .
.
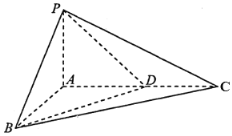
(1)当![]() ,求二面角P-BD-C的余弦值;
,求二面角P-BD-C的余弦值;
(2)若直线PC与平面PBD所成角的正弦值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数),以原点
为参数),以原点![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴建立极坐标系,曲线
轴非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设点![]() ,
,![]() 分别是曲线
分别是曲线![]() ,
,![]() 上两动点且
上两动点且![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() :
:![]() ,点
,点![]() ,
,![]() ,点
,点![]() 在圆
在圆![]() 上,
上,![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)直线![]() 与圆
与圆![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() 点在
点在![]() 轴上方),点
轴上方),点![]() 是抛物线
是抛物线![]() 上的动点,点
上的动点,点![]() 为
为![]() 的外心,求线段
的外心,求线段![]() 长度的最大值,并求出当线段
长度的最大值,并求出当线段![]() 长度最大时,
长度最大时,![]() 外接圆的标准方程.
外接圆的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
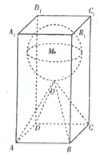
【题目】在日常生活中,石子是我们经常见到的材料,比如在各种建筑工地或者建材市场上常常能看到堆积如山的石子,它的主要成分是碳酸钙.某雕刻师计划在底面边长为2m、高为4m的正四棱柱形的石料![]() 中,雕出一个四棱锥
中,雕出一个四棱锥![]() 和球M的组合体,其中O为正四棱柱的中心,当球的半径r取最大值时,该雕刻师需去除的石料约重___________kg.(最后结果保留整数,其中
和球M的组合体,其中O为正四棱柱的中心,当球的半径r取最大值时,该雕刻师需去除的石料约重___________kg.(最后结果保留整数,其中![]() ,石料的密度
,石料的密度![]() ,质量
,质量![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有7个球,其中红色球2个(同色不加区分),白色,黄色,蓝色,紫色,灰色球各1个,将它们排成一行,要求最左边不排白色,2个红色排一起,黄色和红色不相邻,则有________种不同的排法(用数字回答).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天上有些恒星的亮度是会变化的,其中一种称为造父(型)变星,本身体积会膨胀收缩造成亮度周期性的变化.第一颗被描述的经典造父变星是在1784年.
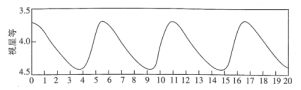
上图为一造父变星的亮度随时间的周期变化图,其中视星等的数值越小,亮度越高,则此变星亮度变化的周期、最亮时视星等,分别约是( )
A.5.5,3.7B.5.4,4.4C.6.5,3.7D.5.5,4.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校高三大理班周三上午四节、下午三节有六门科目可供安排,其中语文和数学各自都必须上两节而且两节连上,而英语、物理、化学、生物最多上一节,则不同的功课安排有________种情况.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com