
分析 理清集合A、B的关系,得到关于m的不等式,解得即可求实数m的取值范围.
解答 解:(1)集合A={-2≤x≤3},B={x|m+1≤x≤2m-1},且B⊆A
①B=∅时,m+1>2m-1,故m<2;
②B≠∅时,m≥2,且$\left\{\begin{array}{l}{m+1≥-2}\\{2m-1≤3}\end{array}\right.$,∴m=2;
故m≤2;
(2)集合A={-2≤x≤3},B={x|m+1≤x≤2m-1},且A⊆B,
∴$\left\{\begin{array}{l}{m+1≤-2}\\{2m-1≥3}\\{m+1≤2m-1}\end{array}\right.$,
解得m∈∅;
(3)若A=B,则m+1=-2且2m-1=3,解得m∈∅.
点评 本题主要考查集合的相等等基本运算,属于基础题.要正确判断两个集合间相等的关系,必须对集合的相关概念有深刻的理解,善于抓住代表元素,认清集合的特征.


科目:高中数学 来源: 题型:选择题
| A. | a${\;}^{\frac{m}{n}}$=($\root{n}{a}$)m | B. | -a${\;}^{\frac{m}{n}}$=$\root{n}{(-a)^{n}}$ | C. | a${\;}^{-\frac{m}{n}}$=$\root{m}{{a}^{n}}$ | D. | a${\;}^{-\frac{m}{n}}$=$\root{n}{{a}^{-m}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
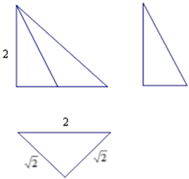 一个几何体的三视图如图.该几何体的各个顶点都在球O的球面上,球O的体积为( )
一个几何体的三视图如图.该几何体的各个顶点都在球O的球面上,球O的体积为( )| A. | $\frac{\sqrt{2}}{3}$π | B. | $\frac{4\sqrt{2}}{3}$π | C. | $\frac{8\sqrt{2}}{3}$π | D. | $\frac{10\sqrt{2}}{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com