
【题目】根据以往的经验,某工程施工期间的将数量X(单位:mm)对工期的影响如下表:
降水量X | X<300 | 300≤X<700 | 700≤X<900 | X≥900 |
工期延误天数Y | 0 | 2 | 6 | 10 |
历年气象资料表明,该工程施工期间降水量X小于300,700,900的概率分别为0.3,0.7,0.9,求:
(I)工期延误天数Y的均值与方差;
(Ⅱ)在降水量X至少是300的条件下,工期延误不超过6天的概率.
【答案】(I)由题意,P(X<300)=0.3,P(300≤X<700)=P(X<700)﹣P(X<300)=0.7﹣0.3=0.4,P(700≤X<900)=P(X<900)﹣P(X<700)=0.9﹣0.7=0.2,P(X≥900)=1﹣0.9=0.1
Y的分布列为
Y | 0 | 2 | 6 | 10 |
P | 0.3 | 0.4 | 0.2 | 0.1 |
∴E(Y)=0×0.3+2×0.4+6×0.2+10×0.1=3
D(Y)=(0﹣3)2×0.3+(2﹣3)2×0.4+(6﹣3)2×0.2+(10﹣3)2×0.1=9.8
∴工期延误天数Y的均值为3,方差为9.8;
(Ⅱ)P(X≥300)=1﹣P(X<300)=0.7,P(300≤X<900)=P(X<900)﹣P(X<300)=0.9﹣0.3=0.6
由条件概率可得P(Y≤6|X≥300)= ![]() .
.
【解析】(I)由题意,该工程施工期间降水量X小于300,700,900的概率分别为0.3,0.7,0.9,结合某程施工期间的降水量对工期的影响,可求相应的概率,进而可得期延误天数Y的均值与方差;(Ⅱ)利用概率的加法公式可得P(X≥300)=1﹣P(X<300)=0.7,P(300≤X<900)=P(X<900)﹣P(X<300)=0.9﹣0.3=0.6,利用条件概率,即可得到结论


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】“郑一”号宇宙飞船返回舱顺利到达地球后,为了及时将航天员救出,地面指挥中心的在返回舱预计到达的区域安排了同一条直线上的三个救援中心(记为![]() ).当返回舱距地面1万米的
).当返回舱距地面1万米的![]() 点的时(假定以后垂直下落,并在
点的时(假定以后垂直下落,并在![]() 点着陆),
点着陆),![]() 救援中心测得飞船位于其南偏东60°方向,仰角为60°,
救援中心测得飞船位于其南偏东60°方向,仰角为60°,![]() 救援中心测得飞船位于其南偏西30°方向,仰角为30°,
救援中心测得飞船位于其南偏西30°方向,仰角为30°,![]() 救援中心测得着陆点
救援中心测得着陆点![]() 位于其正东方向.
位于其正东方向.
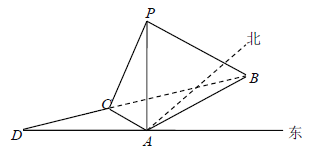
(1)求![]() 两救援中心间的距离;
两救援中心间的距离;
(2)![]() 救援中心与着陆点
救援中心与着陆点![]() 间的距离.
间的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=2x3-3(a+1)x2+6ax+8,其中a∈R.
(1)若f(x)在x=3处取得极值,求常数a的值;
(2)若f(x)在(-∞,0)上为增函数,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn,且Sn=4an﹣p,其中p是不为零的常数.
(1)证明:数列{an}是等比数列;
(2)当p=3时,若数列{bn}满足bn+1=bn+an(n∈N*),b1=2,求数列{bn}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为内角A,B,C所对边的边长,且C=![]() ,a+b=λc(其中λ>1).
,a+b=λc(其中λ>1).
(1)若λ=![]() 时,证明:△ABC为直角三角形;
时,证明:△ABC为直角三角形;
(2)若![]() ·
·![]() =
=![]() λ2,且c=3,求λ的值.
λ2,且c=3,求λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四面体ABCD中,AB,BC,BD两两垂直,BC=BD=2,点E是CD的中点,异面直线AD与BE所成角的余弦值为![]() ,则直线BE与平面ACD所成角的正弦值为( )
,则直线BE与平面ACD所成角的正弦值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C所对的边分别为a,b,c.向量 ![]() =(a,
=(a, ![]() b)与
b)与 ![]() =(cosA,sinB)平行.
=(cosA,sinB)平行.
(1)求A;
(2)若a= ![]() ,b=2,求△ABC的面积.
,b=2,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为  (t为参数),曲线C的极坐标方程是ρcos2θ=sinθ,以极点为原点,极轴为x轴正方向建立直角坐标系,点M(﹣1,0),直线l与曲线C交于A、B两点.
(t为参数),曲线C的极坐标方程是ρcos2θ=sinθ,以极点为原点,极轴为x轴正方向建立直角坐标系,点M(﹣1,0),直线l与曲线C交于A、B两点.
(1)写出直线l的极坐标方程与曲线C普通方程;
(2)线段MA,MB长度分别记为|MA|,|MB|,求|MA||MB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一台机器生产某种产品,如果生产出一件甲等品可获利50元,生产出一件乙等品可获利30元,生产出一件次品,要赔20元,已知这台机器生产出甲等品、乙等品和次品的概率分别为0.6,0.3,和0.1,则这台机器每生产一件产品平均预期可获利________元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com