
【题目】已知点![]() 为圆
为圆![]() ,
, ![]() ,
, ![]() 是圆上的动点,线段
是圆上的动点,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设![]() ,
, ![]() ,过点
,过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于点
交于点![]() (异于点
(异于点![]() ),过点
),过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,直线
,直线![]() 与
与![]() 倾斜角互补.
倾斜角互补.
①直线![]() 的斜率是否为定值?若是,求出该定值;若不是,说明理由;
的斜率是否为定值?若是,求出该定值;若不是,说明理由;
②设![]() 与
与![]() 的面积之和为
的面积之和为![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)本问考查曲线轨迹方程的求法,画出图形分析可有, ![]() ,于是点
,于是点![]() 的轨迹是以点
的轨迹是以点![]() 为焦点,焦距为
为焦点,焦距为![]() ,长轴为
,长轴为![]() 的椭圆,可求出方程;(2)①本问考查直线与椭圆的位置关系,由于直线
的椭圆,可求出方程;(2)①本问考查直线与椭圆的位置关系,由于直线![]() 与
与![]() 倾斜角互补,所以斜率互为相反数,设
倾斜角互补,所以斜率互为相反数,设![]() 的方程为
的方程为![]() ,与椭圆方程联立,消元,得到关于x的一元二次方程,根据韦达定理可以求出点M的坐标,设
,与椭圆方程联立,消元,得到关于x的一元二次方程,根据韦达定理可以求出点M的坐标,设![]() 的方程为
的方程为![]() ,同理可以求出点N的坐标,于是可以求出直线MN的斜率,并判断是否为定值;②由于直线MN的斜率为定值,所以设直线
,同理可以求出点N的坐标,于是可以求出直线MN的斜率,并判断是否为定值;②由于直线MN的斜率为定值,所以设直线![]() 的方程为
的方程为![]() ,与椭圆方程联立,求出弦长
,与椭圆方程联立,求出弦长![]() ,再分别求点A,B到直线MN的距离,于是可以得到
,再分别求点A,B到直线MN的距离,于是可以得到![]() 与
与![]() 的面积之和为
的面积之和为![]() ,再讨论求出取值范围.
,再讨论求出取值范围.
试题解析:(1)由题意![]() .
.
∴点![]() 的轨迹是以点
的轨迹是以点![]() 为焦点,焦距为
为焦点,焦距为![]() ,长轴为
,长轴为![]() 的椭圆,
的椭圆,
所以![]() ,
,
所以点![]() 的轨迹方程是
的轨迹方程是![]()
(2)①设![]() 的方程为
的方程为![]() , 联立方程
, 联立方程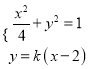 ,得
,得
![]() ,
,
设![]() 与椭圆除
与椭圆除![]() 外的另一个交点
外的另一个交点![]() ,则
,则![]() ,
, ![]() ,
,
代入![]() 的方程得
的方程得![]() ,所以
,所以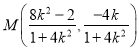 ,
,
因为![]() 倾斜角互补,所以
倾斜角互补,所以![]() 的方程为
的方程为![]() ,
,
联立方程组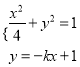 ,得
,得![]() ,
,
设![]() 与椭圆除
与椭圆除![]() 外的另一个交点
外的另一个交点![]() ,则
,则![]() ,
, ![]() ,
,
代入![]() 的方程得
的方程得![]() ,所以
,所以 ,
,
∴直线![]() 的斜率为
的斜率为![]() .
.
②设直线![]() 的方程为
的方程为![]() ,联立方程
,联立方程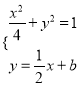 ,得
,得![]() ,
,
由![]() 得
得![]() ,设
,设![]() ,则
,则![]() ,
,
∴![]() .
.
设![]() 分别为点
分别为点![]() 到直线
到直线![]() 的距离, 则
的距离, 则![]()
![]()
![]() ,
,
当![]() 时,
时, ![]()
![]() ,
,
当![]() 时,
时, ![]()
![]() ,
,
当![]() 时,
时, ![]()
![]() ,
,
∴![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】在△ABC中,点A(1,1),B(0,﹣2),C(4,2),D为AB的中点,DE∥BC. (Ⅰ)求BC边上的高所在直线的方程;
(Ⅱ)求DE所在直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各式的大小关系正确的是( )
A.sin11°>sin168°
B.sin194°<cos160°
C.tan(﹣ ![]() )<tan(﹣
)<tan(﹣ ![]() )
)
D.cos(﹣ ![]() )>cos
)>cos ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一某班的一次数学测试成绩(满分为100分)的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图,据此解答如下问题; 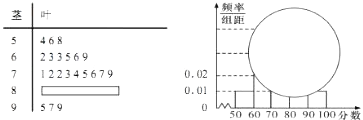
(1)求分数在[50,60)的频率及全班的人数;
(2)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;
(3)根据频率分布直方图,估计该班数学成绩的平均数与中位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测试后,一位老师从本班48同学中随机抽取6位同学,他们的语文、历史成绩如下表:
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 |
语文成绩 | 60 | 70 | 74 | 90 | 94 | 110 |
历史成绩 | 58 | 63 | 75 | 79 | 81 | 88 |
(1)若规定语文成绩不低于90分为优秀,历史成绩不低于80分为优秀,以频率作概率,分别估计该班语文、历史成绩优秀的人数;
(2)用上表数据画出散点图易发现历史成绩![]() 与语文成绩
与语文成绩![]() 具有较强的线性相关关系,求
具有较强的线性相关关系,求![]() 与
与![]() 的线性回归方程(系数精确到0.1).
的线性回归方程(系数精确到0.1).
参考公式:回归直线方程是![]() ,其中
,其中![]() ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 过两点
过两点![]() ,
, ![]() ,且圆心
,且圆心![]() 在直线
在直线![]() 上.
上.
(Ⅰ)求圆![]() 的标准方程;
的标准方程;
(Ⅱ)直线![]() 过点
过点![]() 且与圆
且与圆![]() 有两个不同的交点
有两个不同的交点![]() ,
, ![]() ,若直线
,若直线![]() 的斜率
的斜率![]() 大于0,求
大于0,求![]() 的取值范围;
的取值范围;
(Ⅲ)在(Ⅱ)的条件下,是否存在直线![]() 使得弦
使得弦![]() 的垂直平分线过点
的垂直平分线过点![]() ,若存在,求出直线
,若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱台![]() 的上下底面分别是边长为2和4的正方形,
的上下底面分别是边长为2和4的正方形, ![]() = 4且
= 4且 ![]() ⊥底面
⊥底面![]() ,点
,点![]() 为
为![]() 的中点.
的中点.
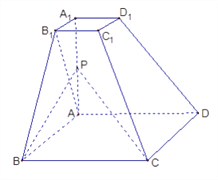
(Ⅰ)求证: ![]() 面
面 ![]() ;
;
(Ⅱ)在![]() 边上找一点
边上找一点![]() ,使
,使![]() ∥面
∥面![]() ,
,
并求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分12分)一块长为![]() 、宽为
、宽为![]() 的长方形铁片,铁片的四角截去四个边长均为
的长方形铁片,铁片的四角截去四个边长均为![]() 的小正方形,然后做成一个无盖方盒.
的小正方形,然后做成一个无盖方盒.
(Ⅰ)试把方盒的容积V表示为![]() 的函数;
的函数;
(Ⅱ)试求方盒容积V的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com