
【题目】[选修4—4:坐标系与参数方程]
以平面直角坐标系的原点为极点,x轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位.已知直线l的参数方程是![]() (t为参数),圆C的极坐标方程是ρ=4cos θ,求直线l被圆C截得的弦长.
(t为参数),圆C的极坐标方程是ρ=4cos θ,求直线l被圆C截得的弦长.
 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
【题目】斜率为![]() 的直线
的直线![]() 过抛物线
过抛物线![]() 的焦点
的焦点![]() ,且与抛物线
,且与抛物线![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)设点![]() 在第一象限,过
在第一象限,过![]() 作抛物线
作抛物线![]() 的准线的垂线,
的准线的垂线,![]() 为垂足,且
为垂足,且![]() ,直线
,直线![]() 与直线
与直线![]() 关于直线
关于直线![]() 对称,求直线
对称,求直线![]() 的方程;
的方程;
(2)过![]() 且与
且与![]() 垂直的直线
垂直的直线![]() 与圆
与圆![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() 与
与![]() 面积之和为
面积之和为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,已知直线l的参数方程为: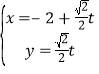 ,
,![]() 为参数
为参数![]() 点的极坐标为
点的极坐标为![]() ,曲线C的极坐标方程为
,曲线C的极坐标方程为![]() .
.
![]() Ⅰ
Ⅰ![]() 试将曲线C的极坐标方程化为直角坐标方程,并求曲线C的焦点在直角坐标系下的坐标;
试将曲线C的极坐标方程化为直角坐标方程,并求曲线C的焦点在直角坐标系下的坐标;
![]() Ⅱ
Ⅱ![]() 设直线l与曲线C相交于两点A,B,点M为AB的中点,求
设直线l与曲线C相交于两点A,B,点M为AB的中点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() 为自然对数的底数).
为自然对数的底数).
(1)若![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的最大值;
上的最大值;
(2)若![]() ,关于
,关于![]() 的方程
的方程![]() 有且仅有一个根, 求实数
有且仅有一个根, 求实数![]() 的取值范围;
的取值范围;
(3)若对任意![]() ,不等式
,不等式![]() 均成立, 求实数
均成立, 求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥![]() 的底面是等腰梯形,
的底面是等腰梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为等边三角形,且点P在底面
为等边三角形,且点P在底面![]() 上的射影为
上的射影为![]() 的中点G,点E在线段
的中点G,点E在线段![]() 上,且
上,且![]() .
.
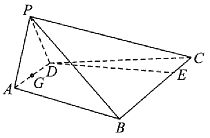
(1)求证:![]() 平面
平面![]() .
.
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在P地正西方向16km的A处和正东方向2km的B处各一条正北方向的公路AC和BD,现计划在AC和BD路边各修建一个物流中心E和F.
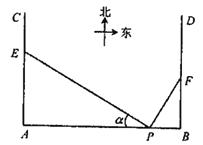
(1)若在P处看E,F的视角![]() ,在B处看E测得
,在B处看E测得![]() ,求AE,BF;
,求AE,BF;
(2)为缓解交通压力,决定修建两条互相垂直的公路PE和PF,设![]() ,公路PF的毎千米建设成本为a万元,公路PE的毎千米建设成本为8a万元.为节省建设成本,试确定E,F的位置,使公路的总建设成本最小.
,公路PF的毎千米建设成本为a万元,公路PE的毎千米建设成本为8a万元.为节省建设成本,试确定E,F的位置,使公路的总建设成本最小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com