练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图所示，在空间四边形ABCD中，已知AD=1，BC=，且AD⊥BC，对角线BD=，AC=，求AC和BD所成的角的大小．
    解：如图所示，分别取AD，CD，AB，DB的中点E，F，G，H，
    连结EF，FH，HG，GE，GF，
    则由三角形中位线定理知EF∥AC且EF=
    GE∥BD且GE=
    GH∥AD，GH=
    HF∥BC，HF=
    从而可知GE与EF所成的锐角(或直角)即为AC和BD所成的角，
    GH和HF所成的锐角(或直角)即为AD与BC所成的角，
    ∵AD⊥BC，
    ∴∠GHF=90°，
    ∴GF2=GH2+HF2=1，
    在△EFG中，EG2+EF2=1=GF2，
    ∴∠GEF=90°，即AC与BD所成的角为90°。
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：四川省双流中学2011－2012学年高二上学期期中考试数学文科试题 题型：013

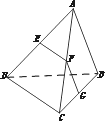
    如图所示，在空间四边形ABCD中，EF∥BC，FG∥AD，则的值为：

    [　　]
    A．

    2

    B．

    1

    C．

    D．

    不确定

    查看答案和解析>>

    科目：高中数学 来源：四川省双流中学2011－2012学年高二上学期期中考试数学理科试题 题型：013

    如图所示，在空间四边形ABCD中，EF∥BC，FG∥AD，则的值为：

    [　　]
    A．

    2

    B．

    1

    C．

    D．

    不确定

    查看答案和解析>>

    科目：高中数学 来源：学习高手必修二数学苏教版 苏教版 题型：044

    如图所示，在空间四边形ABCD中，各边长及对角线长都是a，点M、N分别是BC、AD的中点，求异面直线CN、DM所成角的余弦．

    查看答案和解析>>

    科目：高中数学 来源：数学教研室 题型：013

    如图所示，在空间四边形ABCD中，E、F分别为边AB、AD上的点，且AE∶EB=AF∶FD=1∶4，又H、G分别为BC、CD的中点，则

    [　　]

    A．BD∥平面EFGH，且EFGH是矩形

    B．EF∥平面BCD，且EFGH是梯形

    C．HG∥平面ABD，且EFGH是菱形

    D．EH∥平面ADC，且EFGH是平行四边形．

    查看答案和解析>>

    科目：高中数学 来源： 题型：013

    如图所示，在空间四边形ABCD中，E、F分别为边AB、AD上的点，且AE∶EB=AF∶FD=1∶4，又H、G分别为BC、CD的中点，则

    [　　]

    A．BD∥平面EFGH，且EFGH是矩形

    B．EF∥平面BCD，且EFGH是梯形

    C．HG∥平面ABD，且EFGH是菱形

    D．EH∥平面ADC，且EFGH是平行四边形．

    查看答案和解析>>

    同步练习册答案