Question

【题目】已知数列{an}的通项公式为an= ，n∈N*
（1）求数列{ }的前n项和Sn
（2）设bn=anan+1 ， 求{bn}的前n项和Tn ．

Answer 1

【答案】
（1）解：由an= ，n∈N*，

∴ = =4n﹣1，

∴数列{ }是以3为首项，以4为公差的等差数列，

∴数列{ }的前n项和Sn= =2n2+n

（2）解：bn=anan+1= = （ ﹣ ），

∴{bn}的前n项和Tn，Tn=b1+b2+b3+…+bn，

= [（1﹣ ）+（ ﹣ ）+（ ﹣ ）+…+（ ﹣ ）]，

= （1﹣ ），

= ，

Tn=

【解析】（1）由an= ，n∈N* ， 则 = =4n﹣1，数列{ }是以3为首项，以4为公差的等差数列，根据等差数列前n项和公式，即可求得Sn；（2）由bn=anan+1= = （ ﹣ ），采用“裂项法”，即可求得{bn}的前n项和Tn ．
【考点精析】关于本题考查的数列的前n项和和数列的通项公式，需要了解数列{an}的前n项和sn与通项an的关系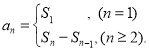；如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式才能得出正确答案．