
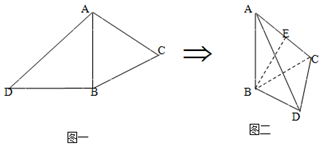
 如图一,△ABC是正三角形,△ABD是等腰直角三角形,AB=BD=2.将△ABD沿AB折起,使得面ABD⊥面ABC,如图二,E为AC的中点
如图一,△ABC是正三角形,△ABD是等腰直角三角形,AB=BD=2.将△ABD沿AB折起,使得面ABD⊥面ABC,如图二,E为AC的中点分析 (Ⅰ)证明BD⊥面ABC,即可证明BD⊥AC;
(Ⅱ)证明AC⊥DE,即可求△ADC的面积;
(Ⅲ)利用等体积转化,即可求三棱锥A-BDE的体积.
解答 (Ⅰ)证明:∵面ABD⊥面ABC,面ABD∩面ABC=AB,BD?面ABD,BD⊥AB,
∴BD⊥面ABC,
又∵AC?面ABC,∴BD⊥AC …(4分)
(Ⅱ)解:∵BD⊥面ABC,BC?面ABC,∴BD⊥BC,
在Rt△DBC中,BC=BA=2,BD=2,
∴DC=2$\sqrt{2}$,
因为BD⊥面ABC,△ABC是正三角形,E为AC的中点,
∴AC⊥BE,AC⊥BD⇒AC⊥面BED⇒AC⊥DE
∴$△ABC中BE=\sqrt{3},在Rt△BDE中,DE=\sqrt{B{D^2}+B{E^2}}=\sqrt{4+3}=\sqrt{7}$
∴${S_{△ADC}}=\frac{1}{2}AC×ED=\frac{1}{2}×2×\sqrt{7}=\sqrt{7}$…(8分)
(Ⅲ)解:${V_{A-BDE}}={V_{D-ABE}}=\frac{1}{3}{S_{△ABE}}×BD=\frac{1}{3}×\frac{1}{2}×AE×BE×BD=\frac{1}{6}×1×\sqrt{3}×2=\frac{{\sqrt{3}}}{3}$.
…(12分)
点评 本题考查线面垂直的证明,考查三角形面积的求法,考查体积的求法,正确运用线面垂直的判定定理是关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [3,+∞) | B. | [2,+∞) | C. | (3,+∞) | D. | (一∞,-3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
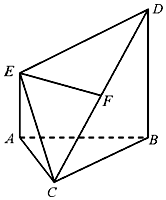 如图,BD⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE=2,F为CD中点.
如图,BD⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE=2,F为CD中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
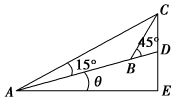 如图所示,在坡度一定的山坡A处测得山顶上一建筑物CD的顶端C对于山坡的斜度为15°,向山顶前进100m到达B处,又测得C对于山坡的斜度为45°,若CD=50m,山坡对于地平面的坡度为θ,则cosθ=$\sqrt{3}$-1.
如图所示,在坡度一定的山坡A处测得山顶上一建筑物CD的顶端C对于山坡的斜度为15°,向山顶前进100m到达B处,又测得C对于山坡的斜度为45°,若CD=50m,山坡对于地平面的坡度为θ,则cosθ=$\sqrt{3}$-1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com