练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

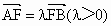    (2006全国Ⅱ，21)已知抛物线的焦点为F，A、B是抛物线上的两动点，且．过A、B两点分别作抛物线的切线，设其交点为M．

    (1)证明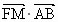：为定值；

    (2)设△ABM的面积为S，写出S=f(λ)的表达式，并求S的最小值．

    答案：略
    解析：

    解析：(1)由已知条件，得F(0，1)，λ＞0．

    设，．由，

    即得，

    将①式两边平方并把，

    代入得，　　　　　　③

    解②、③式得，，且有．

    抛物线方程为．求导得．

    所以过抛物线上A、B两点的切线方程分别是，

    ，即，．

    解出两条切线的交点M的坐标为．

    所以，

    ，

    所以为定值，其值为0．

    (2)由(1)知在△ABM中，FM⊥AB，因而．

    ．

    因为|AF|、|BF|分别等于A、B到抛物线准线y=－1的距离，所以

    ．

    于是，

    由，知S≥4，

    且当λ=1时，S取得最小值4．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：044

    (2006全国Ⅱ，22)设数列的前n项和为，且方程有一根为，n=1、2、3…．

    (1)求，；

    (2)求的通项公式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：044

    (2006全国Ⅰ，21)已知函数．

    (1)设a＞0，讨论y=f(x)的单调性；

    (2)若对任意x(0，1)恒有f(x)＞1，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：022

    (2006全国Ⅱ，16)一个社会调查机构就某地居民的月收入调查了10 000人，并根据所得数据画了样本的频率分布直方图(如图所示)．为了分析居民的收入与年龄、学历、职业等方面的关系，要从这10 000人中再用分层抽样方法抽出100人作进一步调查，则在[2 500，3 000)(元)月收入段应抽出__________人．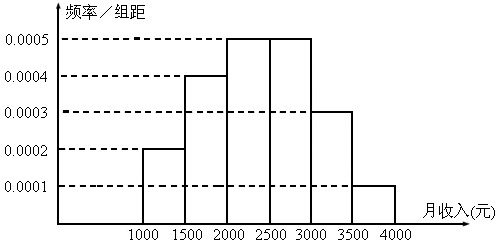

    查看答案和解析>>

    科目：高中数学 来源： 题型：013

    (2006全国Ⅱ，7)如下图，平面α⊥平面β，Aα，Bβ，AB与两平面α、β所成的角分别为和．过A、B分别作两平面交线的垂线，垂足为、，则AB∶等于

    [　　]

    A．2∶1

    B．3∶1

    C，3∶2

    D．4∶3

    查看答案和解析>>

    同步练习册答案