
【题目】二次函数y=ax2+bx+c(x∈R)的部分对应值如表:
x | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 |
y | ﹣6 | 0 | 4 | 6 | 6 | 4 | 0 | ﹣6 |
则一元二次不等式ax2+bx+c>0的解集是( )
A.{x|x<﹣2,或x>3}
B.{x|x≤﹣2,或x≥3}
C.{x|﹣2<x<3}
D.{x|﹣2≤x≤3}
 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:
【题目】已知命题:“x∈{x|﹣1≤x≤1},都有不等式x2﹣x﹣m<0成立”是真命题.
(1)求实数m的取值集合B;
(2)设不等式(x﹣3a)(x﹣a﹣2)<0的解集为A,若x∈A是x∈B的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某位同学在2015年5月进行社会实践活动,为了对白天平均气温与某奶茶店的某种饮料销量之间的关系进行分析研究,他分别记录了5月1日至5月5日的白天平均气温x(°C)与该奶茶店的这种饮料销量y(杯),得到如下数据:
日 期 | 5月1日 | 5月2日 | 5月3日 | 5月4日 | 5月5日 |
平均气温x(°C) | 9 | 10 | 12 | 11 | 8 |
销量y(杯) | 23 | 25 | 30 | 26 | 21 |
(1)若从这五组数据中随机抽出2组,求抽出的2组数据不是相邻2天数据的概率;
(2)请根据所给五组数据,求出y关于x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() .
.
(参考公式: ![]() =
= 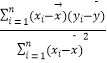 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京是我国严重缺水的城市之一.为了倡导“节约用水,从我做起”,小明在他所在学校的2000名同学中,随机调查了40名同学家庭中一年的月均用水量(单位:吨),并将月均用水量分为6组:[2,4),[4,6),[6,8),[8,10),[10,12),[12,14]加以统计,得到如图所示的频率分布直方图. 
(Ⅰ)给出图中实数a的值;
(Ⅱ)根据样本数据,估计小明所在学校2000名同学家庭中,月均用水量低于8吨的约有多少户;
(Ⅲ)在月均用水量大于或等于10吨的样本数据中,小明决定随机抽取2名同学家庭进行访谈,求这2名同学中恰有1人所在家庭的月均用水量属于[10,12)组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个不重合的平面α,β和两条不同直线m,n,则下列说法正确的是( )
A.若m⊥n,n⊥α,mβ,则α⊥β
B.若α∥β,n⊥α,m⊥β,则m∥n
C.若m⊥n,nα,mβ,则α⊥β
D.若α∥β,nα,m∥β,则m∥n
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需要增加投入100元,最大月产量是400台.已知总收益满足函数 ![]() ,其中x是仪器的月产量(单位:台).
,其中x是仪器的月产量(单位:台).
(1)将利润y(单位:元)表示为月产量x(单位:台)的函数;
(2)当月产量为何值时,公司所获得利润最大?最大利润为多少?(总收益=总成本+利润).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数g(x)=aln x,f(x)=x3+x2+bx.
(1)若f(x)在区间[1,2]上不是单调函数,求实数b的范围;
(2)若对任意x∈[1,e],都有g(x)≥﹣x2+(a+2)x恒成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com