
【题目】(Ⅰ)比较下列两组实数的大小: ① ![]() ﹣1与2﹣
﹣1与2﹣ ![]() ;②2﹣
;②2﹣ ![]() 与
与 ![]() ﹣
﹣ ![]() ;
;
(Ⅱ)类比以上结论,写出一个更具一般意义的结论,并给出证明.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设命题p:x0∈(0,+∞),3 ![]() +x0=2016,命题q:a∈(0,+∞),f(x)=|x|﹣ax,(x∈R)为偶函数,那么,下列命题为真命题的是( )
+x0=2016,命题q:a∈(0,+∞),f(x)=|x|﹣ax,(x∈R)为偶函数,那么,下列命题为真命题的是( )
A.p∧q
B.(¬p)∧q
C.p∧(¬q)
D.(¬p)∧(¬q)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设b和c分别是先后抛掷一枚骰子得到的点数,用随机变量ξ表示方程x2+bx+c=0实根的个数(重根按一个计).
(1)求方程x2+bx+c=0有实根的概率;
(2)(理)求ξ的分布列和数学期望 (文)求P(ξ=1)的值
(3)(理)求在先后两次出现的点数中有5的条件下,方程x2+bx+c=0有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设b和c分别是先后抛掷一枚骰子得到的点数,用随机变量ξ表示方程x2+bx+c=0实根的个数(重根按一个计).
(1)求方程x2+bx+c=0有实根的概率;
(2)(理)求ξ的分布列和数学期望 (文)求P(ξ=1)的值
(3)(理)求在先后两次出现的点数中有5的条件下,方程x2+bx+c=0有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 表示两条不同的直线,
表示两条不同的直线, ![]() 表示一个平面,给出下列四个命题:
表示一个平面,给出下列四个命题:
① ![]() ;②
;② ![]() ;
;
③ ![]() ;④
;④ ![]() .
.
其中正确命题的序号是( )
A.①②
B.②③
C.②④
D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
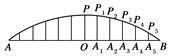
【题目】某圆拱桥的示意图如图所示,该圆拱的跨度AB是36 m,拱高OP是6 m,在建造时,每隔3 m需用一个支柱支撑,求支柱A2P2的长.(精确到0.01 m)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com