练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】【2016高考北京文数】已知椭圆C：过点A（2,0），B（0,1）两点.

    （I）求椭圆C的方程及离心率；

    （Ⅱ）设P为第三象限内一点且在椭圆C上，直线PA与y轴交于点M，直线PB与x轴交于点N，求证：四边形ABNM的面积为定值.

    【答案】（Ⅰ）；（Ⅱ）见解析.

    【解析】

    试题分析：（Ⅰ）根据两顶点坐标可知a,b的值，则亦知椭圆方程，根据椭圆性质及离心率公式求解；（Ⅱ）四边形的面积等于对角线乘积的一半，分别求出对角线的值求乘积为定值即可.

    试题解析：（I）由题意得，，．

    所以椭圆的方程为．

    又，

    所以离心率．

    （II）设（，），则．

    又，，所以，

    直线的方程为．

    令，得，从而．

    直线的方程为．

    令，得，从而．

    所以四边形的面积

    ．

    从而四边形的面积为定值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】气象意义上，从春季进入夏季的标志为：“连续5天的日平均温度不低于22℃”.现有甲、乙、丙三地连续5天的日平均温度的记录数据（记录数据都是正整数）：

    ①甲地：5个数据的中位数为24，众数为22；

    ②乙地：5个数据的中位数为27，总体均值为24；

    ③丙地：5个数据的中有一个数据是32，总体均值为26，总体方差为10.8；

    则肯定进入夏季的地区的有（ ）

    A. ①②③ B. ①③ C. ②③ D. ①

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：极坐标与参数方程

    已知平面直角坐标系，以为极点， 轴的非负半轴为极轴建立极坐标系，曲线的参数方程为为参数）. 点是曲线上两点，点的极坐标分别为.

    （1）写出曲线的普通方程和极坐标方程；

    （2）求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】【2016高考浙江文数】如图，设抛物线的焦点为F，抛物线上的点A到y轴的距离等于|AF|-1.

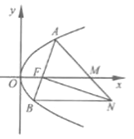
    （I）求p的值；

    （II）若直线AF交抛物线于另一点B，过B与x轴平行的直线和过F与AB垂直的直线交于点N，AN与x

    轴交于点M.求M的横坐标的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】数列{an}的前n项和Sn满足：2Sn=3an﹣6n（n∈N*） （Ⅰ）求数列{an}的通项公式；
    （Ⅱ）设 ，其中常数λ＞0，若数列{bn}为递增数列，求λ的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，内角A，B，C的对边分别为a，b，c，且bsinA= acosB． （Ⅰ）求角B的大小；
    （Ⅱ）若b=3，sinC=2sinA，求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

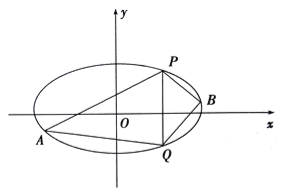
    【题目】【天津市红桥区重点中学八校2017届高三4月联考数学（文）】已知椭圆的中心在原点，离心率等于，它的一个短轴端点恰好是抛物线的焦点

    （1）求椭圆的方程；

    （2）已知、是椭圆上的两点， ， 是椭圆上位于直线两侧的动点.①若直线的斜率为，求四边形面积的最大值；

    ②当， 运动时，满足,试问直线的斜率是否为定值，请说明理由

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （Ⅰ）讨论的单调性；

    （Ⅱ）设，证明：当时， .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （Ⅰ）若与在处相切，试求的表达式；

    （Ⅱ）若在上是减函数，求实数的取值范围；

    （Ⅲ）证明不等式：.

    查看答案和解析>>

    同步练习册答案