
| A. | C${\;}_{10}^{5}$•C${\;}_{10}^{3}$•C${\;}_{10}^{2}$ | B. | C${\;}_{10}^{5}$•C${\;}_{5}^{3}$•C${\;}_{2}^{2}$ | ||
| C. | C${\;}_{5}^{2}$•C${\;}_{10}^{3}$ | D. | C${\;}_{10}^{5}$•C${\;}_{4}^{2}$ |
分析 根据题意,建立数学模型,展开式中含x5y3z2项的系数看作从10个完全相同的小球中依次任选5个,再从余下的5个小球中任取3个,最后从剩下的2个小球中任取2个,不同的方法有多少种.
解答 解:将(x+y+z)10展开后,展开式中含x5y3z2项的系数可以看作:
第一步从10个完全相同的小球中任选5个,有${C}_{10}^{5}$种不同的方法;
第二步从余下的5个小球中任取3个,有${C}_{5}^{3}$不同的方法;
第三步从剩下的2个小球中任取2个,有${C}_{2}^{2}$种不同的方法,
根据分步相乘原理,得出共有${C}_{10}^{5}$•${C}_{5}^{3}$•${C}_{2}^{2}$种不同的方法.
故选:B.
点评 不同考查了二项式定理的应用问题,也考查了数学建模的应用问题,是基础题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 相等 | B. | 前者大 | C. | 后者大 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,1 ) | B. | ( 2,+∞) | C. | ( 0,$\frac{1}{2}$)∪( 2,+∞) | D. | ($\frac{1}{2}$,1 )∪( 2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
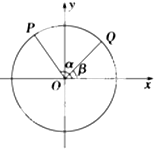 如图,以Ox为始边作角α与β(0<β<α<π),它们的终边分别与单位圆相交于P,Q两点,已知点P的坐标为$({-\frac{3}{5},\frac{4}{5}})$
如图,以Ox为始边作角α与β(0<β<α<π),它们的终边分别与单位圆相交于P,Q两点,已知点P的坐标为$({-\frac{3}{5},\frac{4}{5}})$查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com