
ΓΨΧβΡΩΓΩ»γΆΦΘ§Τχœσ≤ΩΟ≈‘Λ±®Θ§‘ΎΚΘΟφ…œ…ζ≥…ΝΥ“ΜΙ…Ϋœ«ΩΧ®ΖγΘ§‘ΎΨίΧ®Ζγ÷––Ρ60«ßΟΉΒΡ‘≤–Έ«χ”ρΡΎΫΪ ήΒΫ―œ÷ΊΤΤΜΒΘ§Χ®Ζγ÷––Ρ’βΗω¥”ΚΘΑΕMΒψΒ«¬ΫΘ§≤Δ“‘72«ßΟΉ/–Γ ±ΒΡΥΌΕ»―Ί±±ΤΪΈς60ΓψΒΡΖΫœρ“ΤΕ·Θ§“―÷ΣMΒψΈΜ”ΎA≥«ΒΡΡœΤΪΕΪ15ΓψΖΫœρΘ§ΨύA≥« ![]() «ßΟΉΘΜMΒψΈΜ”ΎB≥«ΒΡ’ΐΕΪΖΫœρΘ§ΨύB≥«
«ßΟΉΘΜMΒψΈΜ”ΎB≥«ΒΡ’ΐΕΪΖΫœρΘ§ΨύB≥« ![]() «ßΟΉΘ§ΦΌ…ηΧ®Ζγ‘Ύ“ΤΕ·ΒΡΙΐ≥Χ÷–Θ§ΤδΖγΝΠΚΆΖΫœρ±Θ≥÷≤Μ±δΘ§«κΜΊ¥πœ¬Ν–Έ ΧβΘΚ
«ßΟΉΘ§ΦΌ…ηΧ®Ζγ‘Ύ“ΤΕ·ΒΡΙΐ≥Χ÷–Θ§ΤδΖγΝΠΚΆΖΫœρ±Θ≥÷≤Μ±δΘ§«κΜΊ¥πœ¬Ν–Έ ΧβΘΚ 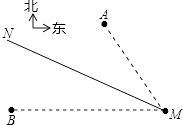
Θ®1Θ©A≥«ΚΆB≥« «ΖώΜα ήΒΫ¥Υ¥ΈΧ®ΖγΒΡ«÷œ°ΘΩ≤ΔΥΒΟςάμ”…ΘΜ
Θ®2Θ©»τ ήΒΫ¥Υ¥ΈΧ®ΖγΒΡ«÷œ°Θ§ΗΡ≥« ήΒΫΧ®Ζγ«÷œ°ΒΡ≥÷–χ ±Φδ”–Εύ…Ό–Γ ±ΘΩ
ΓΨ¥πΑΗΓΩ
Θ®1Θ©ΫβΘΚ…ηΧ®Ζγ÷––Ρ‘Υ––ΒΡ¬ΖœΏΈΣ…δœΏMNΘ§”Ύ «ΓœAMN=60Γψ©¹15Γψ=45ΓψΘ°
ΙΐAΉςAHΓΆMN”ΎHΘ§Ι AMH «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ°
ΓΏAM=61 ![]() Θ§ΓœAMH=60Γψ©¹15Γψ=45ΓψΘ§
Θ§ΓœAMH=60Γψ©¹15Γψ=45ΓψΘ§
ΓύAH=AMsin45Γψ=61ΘΨ60Θ°
ΓύA≥«≤ΜΜα ήΒΫΧ®ΖγΒΡ”ΑœλΘΜ
ΙΐBΉςBH1ΓΆMN”ΎH1Θ°
ΓΏMB=60 ![]() Θ§ΓœBMN=90Γψ©¹60Γψ=30ΓψΘ§
Θ§ΓœBMN=90Γψ©¹60Γψ=30ΓψΘ§
ΓύBH1= ![]() ΓΝ60
ΓΝ60 ![]() ΘΦ60Θ§
ΘΦ60Θ§
“ρ¥ΥB≥«Μα ήΒΫΧ®ΖγΒΡ”ΑœλΘ°
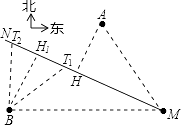
Θ®2Θ©ΫβΘΚ“‘BΈΣ‘≤–Ρ60kmΈΣΑκΨΕΉς‘≤”κMNΫΜ”ΎT1ΓΔT2Θ§‘ρBT1=BT2=60Θ°
‘ΎRtΓςBT1H1÷–Θ§sinΓœBT1H1= ![]() =
= ![]() Θ§
Θ§
ΓύΓœBT1H1=60ΓψΘ°
ΓύΓςBT1T2 «Β»±Ώ»ΐΫ«–ΈΘ°
ΓύT1T2=60Θ°
ΓύΧ®Ζγ÷––ΡΨ≠ΙΐœΏΕΈT1T2…œΥυ”ΟΒΡ ±Φδ ![]() =
= ![]() –Γ ±Θ°
–Γ ±Θ°
“ρ¥ΥB≥« ήΒΫΧ®Ζγ«÷œ°ΒΡ ±ΦδΈΣ ![]() –Γ ±Θ°
–Γ ±Θ°
ΓΨΫβΈωΓΩΘ®1Θ©ΙΐAΉςAHΓΆMN”ΎHΘ§Ι AMH «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§Ω…«σ≥ωAMΘ§‘ρΩ…“‘≈–ΕœA≥« «ΖώΜα ήΒΫ¥Υ¥ΈΧ®ΖγΒΡ«÷œ°Θ° Ά§άμΘ§ΙΐBΉςBH1ΓΆMN”ΎH1 Θ§ «σ≥ωBH1 Θ§ Ω…“‘≈–ΕœB≥« «ΖώΜα ήΒΫ¥Υ¥ΈΧ®ΖγΒΡ«÷œ°Θ°Θ®2Θ©«σΗΟ≥« – ήΒΫΧ®Ζγ«÷œ°ΒΡ≥÷–χ ±ΦδΘ§“‘BΈΣ‘≤–Ρ60kmΈΣΑκΨΕΉς‘≤”κMNΫΜ”ΎT1ΓΔT2 Θ§ ‘ρT1T2ΨΆ «Χ®Ζγ”Αœλ ±Ψ≠ΙΐΒΡ¬ΖΨΕΘ§«σ≥ωΚσ≥ΐ“‘Χ®ΖγΒΡΥΌΕ»ΨΆ « ±ΦδΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ”κ«ζœΏ![]() œύ«–ΒΡ÷±œΏ
œύ«–ΒΡ÷±œΏ![]() Θ§”κ
Θ§”κ![]() ÷αΘ§
÷αΘ§ ![]() ÷αΫΜ”Ύ
÷αΫΜ”Ύ![]() ΝΫΒψΘ§
ΝΫΒψΘ§ ![]() ΈΣ‘≠ΒψΘ§
ΈΣ‘≠ΒψΘ§ ![]() Θ§
Θ§ ![]() Θ§Θ®
Θ§Θ® ![]() Θ©.
Θ©.
Θ®1Θ©«σ÷Λ:ΘΚ ![]() ”κ
”κ![]() œύ«–ΒΡΧθΦΰ «ΘΚ
œύ«–ΒΡΧθΦΰ «ΘΚ ![]() .
.
Θ®2Θ©«σœΏΕΈ![]() ÷–ΒψΒΡΙλΦΘΖΫ≥ΧΘΜ
÷–ΒψΒΡΙλΦΘΖΫ≥ΧΘΜ
Θ®3Θ©«σ»ΐΫ«–Έ![]() ΟφΜΐΒΡΉν–Γ÷Β.
ΟφΜΐΒΡΉν–Γ÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() Θ§
Θ§
![]()
(Δώ)»τ![]() Χ÷¬έ
Χ÷¬έ![]() ΒΡΒΞΒς–‘ΘΜ
ΒΡΒΞΒς–‘ΘΜ
(Δρ)»τΙΐΒψ![]() Ω…ΉςΚ· ΐ
Ω…ΉςΚ· ΐ![]() ΆΦœσΒΡΝΫΧθ≤ΜΆ§«–œΏΘ§«σ Β ΐ
ΆΦœσΒΡΝΫΧθ≤ΜΆ§«–œΏΘ§«σ Β ΐ![]() ΒΡ»Γ÷ΒΖΕΈßΘ°
ΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΆ÷‘≤![]() ΒΡΕ‘≥Τ÷αΈΣΉχ±ξ÷αΘ§άκ–Ρ¬ ΈΣ
ΒΡΕ‘≥Τ÷αΈΣΉχ±ξ÷αΘ§άκ–Ρ¬ ΈΣ![]() Θ§«““ΜΗωΫΙΒψΉχ±ξΈΣ
Θ§«““ΜΗωΫΙΒψΉχ±ξΈΣ![]() Θ°
Θ°
Θ®1Θ©«σΆ÷‘≤![]() ΒΡΖΫ≥ΧΘΜ
ΒΡΖΫ≥ΧΘΜ
Θ®2Θ©…η÷±œΏ![]() ”κΆ÷‘≤
”κΆ÷‘≤![]() œύΫΜ”Ύ
œύΫΜ”Ύ![]() ΝΫΒψΘ§“‘œΏΕΈ
ΝΫΒψΘ§“‘œΏΕΈ![]() ΈΣΝΎ±ΏΉςΤΫ––ΥΡ±Ώ–Έ
ΈΣΝΎ±ΏΉςΤΫ––ΥΡ±Ώ–Έ![]() Θ§Τδ÷–Βψ
Θ§Τδ÷–Βψ![]() ‘ΎΆ÷‘≤
‘ΎΆ÷‘≤![]() …œΘ§
…œΘ§ ![]() ΈΣΉχ±ξ‘≠ΒψΘ§«σΒψ
ΈΣΉχ±ξ‘≠ΒψΘ§«σΒψ![]() ΒΫ÷±œΏ
ΒΫ÷±œΏ![]() ΒΡΨύάκΒΡΉν–Γ÷ΒΘ°
ΒΡΨύάκΒΡΉν–Γ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…η{an}ΈΣΒ»≤ν ΐΝ–Θ§SnΈΣ ΐΝ–{an}ΒΡ«ΑnœνΚΆΘ§“―÷ΣS7=7Θ§S15=75Θ§TnΈΣ ΐΝ– ![]() ΒΡ«ΑnœνΚΆΘ§«σTn Θ°
ΒΡ«ΑnœνΚΆΘ§«σTn Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“Μœ Μ®ΒξΗυΨί“ΜΗω‘¬Θ®30ΧλΘ©Ρ≥÷÷œ Μ®ΒΡ»’œζ έΝΩ”κœζ έΧλ ΐΆ≥ΦΤ»γœ¬Θ§ΫΪ»’œζ έΝΩ¬δ»κΗςΉι«χΦδΤΒ¬ ”ΈΣΗ≈¬ Θ°
»’œζ έΝΩΘ®÷ΠΘ© |
|
|
|
|
|
œζ έΧλ ΐ | 3Χλ | 5Χλ | 13Χλ | 6Χλ | 3Χλ |
Θ®1Θ© ‘«σ’β30Χλ÷–»’œζ έΝΩΒΆ”Ύ100÷ΠΒΡΗ≈¬ ΘΜ
Θ®2Θ©»τ¥ΥΜ®Βξ‘Ύ»’œζ έΝΩΒΆ”Ύ100÷ΠΒΡ ±Κρ―Γ‘ώ2ΧλΉς¥ΌœζΜνΕ·Θ§«σ’β2Χλ«ΓΚΟ «‘Ύ»’œζ έΝΩΒΆ”Ύ50÷Π ±ΒΡΗ≈¬ Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΕ‘”ΎΚ· ΐfΘ®xΘ©=sinΘ®2x+ ![]() Θ©Θ§œ¬Ν–ΟϋΧβΘΚ ΔΌΚ· ΐΆΦœσΙΊ”Ύ÷±œΏx=©¹
Θ©Θ§œ¬Ν–ΟϋΧβΘΚ ΔΌΚ· ΐΆΦœσΙΊ”Ύ÷±œΏx=©¹ ![]() Ε‘≥ΤΘΜ
Ε‘≥ΤΘΜ
ΔΎΚ· ΐΆΦœσΙΊ”ΎΒψΘ® ![]() Θ§0Θ©Ε‘≥ΤΘΜ
Θ§0Θ©Ε‘≥ΤΘΜ
ΔέΚ· ΐΆΦœσΩ…Ω¥Ής «Α―y=sin2xΒΡΆΦœσœρΉσΤΫ“ΤΗω ![]() ΒΞΈΜΕχΒΟΒΫΘΜ
ΒΞΈΜΕχΒΟΒΫΘΜ
ΔήΚ· ΐΆΦœσΩ…Ω¥Ής «Α―y=sinΘ®x+ ![]() Θ©ΒΡΆΦœσ…œΥυ”–ΒψΒΡΚαΉχ±ξΥθΕΧΒΫ‘≠ά¥ΒΡ
Θ©ΒΡΆΦœσ…œΥυ”–ΒψΒΡΚαΉχ±ξΥθΕΧΒΫ‘≠ά¥ΒΡ ![]() ±ΕΘ®ΉίΉχ±ξ≤Μ±δΘ©ΕχΒΟΒΫΘΜΤδ÷–’ΐ»ΖΒΡΟϋΧβ « Θ°
±ΕΘ®ΉίΉχ±ξ≤Μ±δΘ©ΕχΒΟΒΫΘΜΤδ÷–’ΐ»ΖΒΡΟϋΧβ « Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() Θ§«ζœΏ
Θ§«ζœΏ![]() ‘ΎΒψ
‘ΎΒψ![]() ¥ΠΒΡ«–œΏ”κ÷±œΏ
¥ΠΒΡ«–œΏ”κ÷±œΏ![]() ¥Ι÷±Θ®Τδ÷–
¥Ι÷±Θ®Τδ÷–![]() ΈΣΉ‘»ΜΕ‘ ΐΒΡΒΉ ΐΘ©Θ°
ΈΣΉ‘»ΜΕ‘ ΐΒΡΒΉ ΐΘ©Θ°
Θ®IΘ©«σ![]() ΒΡΫβΈω ΫΦΑΒΞΒςΒίΦθ«χΦδΘΜ
ΒΡΫβΈω ΫΦΑΒΞΒςΒίΦθ«χΦδΘΜ
Θ®IIΘ© «Ζώ¥φ‘Ύ≥Θ ΐ![]() Θ§ ΙΒΟΕ‘”ΎΕ®“ε”ρΡΎΒΡ»Έ“β
Θ§ ΙΒΟΕ‘”ΎΕ®“ε”ρΡΎΒΡ»Έ“β![]() Κψ≥…ΝΔΘΩ»τ¥φ‘ΎΘ§«σ≥ω
Κψ≥…ΝΔΘΩ»τ¥φ‘ΎΘ§«σ≥ω![]() ΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ―Γ–ό4-4ΘΚΉχ±ξœΒ”κ≤Έ ΐΖΫ≥Χ
“―÷Σ![]() Θ§‘Ύ÷±Ϋ«Ήχ±ξœΒ
Θ§‘Ύ÷±Ϋ«Ήχ±ξœΒ![]() ÷–Θ§÷±œΏ
÷–Θ§÷±œΏ![]() ΒΡ≤Έ ΐΖΫ≥ΧΈΣ
ΒΡ≤Έ ΐΖΫ≥ΧΈΣ![]() Θ®
Θ®![]() ΈΣ≤Έ ΐΘ©ΘΜ‘Ύ“‘Ήχ±ξ‘≠Βψ
ΈΣ≤Έ ΐΘ©ΘΜ‘Ύ“‘Ήχ±ξ‘≠Βψ![]() ΈΣΦΪΒψΘ§
ΈΣΦΪΒψΘ§ ![]() ÷αΒΡ’ΐΑκ÷αΈΣΦΪ÷αΒΡΦΪΉχ±ξœΒ÷–Θ§÷±œΏ
÷αΒΡ’ΐΑκ÷αΈΣΦΪ÷αΒΡΦΪΉχ±ξœΒ÷–Θ§÷±œΏ![]() ΒΡΦΪΉχ±ξΖΫ≥Χ «
ΒΡΦΪΉχ±ξΖΫ≥Χ «![]() .
.
Θ®ΔώΘ©«σ÷ΛΘΚ ![]() ΘΜ
ΘΜ
Θ®ΔρΘ©…ηΒψ![]() ΒΡΦΪΉχ±ξΈΣ
ΒΡΦΪΉχ±ξΈΣ![]() Θ§
Θ§ ![]() ΈΣ÷±œΏ
ΈΣ÷±œΏ![]() Θ§
Θ§ ![]() ΒΡΫΜΒψΘ§«σ
ΒΡΫΜΒψΘ§«σ![]() ΒΡΉν¥σ÷Β.
ΒΡΉν¥σ÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com