
【题目】如图,在平面直角坐标系xOy中,F1 , F2分别为椭圆 ![]() +
+ ![]() =1(a>b>0)的左、右焦点,顶点B的坐标为(0,b),连接BF2并延长交椭圆于点A,过点A作x轴的垂线交椭圆于另一点C,连接F1C.
=1(a>b>0)的左、右焦点,顶点B的坐标为(0,b),连接BF2并延长交椭圆于点A,过点A作x轴的垂线交椭圆于另一点C,连接F1C. 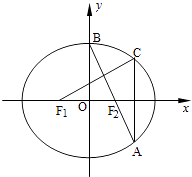
(1)若点C的坐标为( ![]() ,
, ![]() ),且BF2=
),且BF2= ![]() ,求椭圆的方程;
,求椭圆的方程;
(2)若F1C⊥AB,求椭圆离心率e的值.
【答案】
(1)解:∵C的坐标为( ![]() ,
, ![]() ),
),
∴ ![]() ,即
,即 ![]() ,
,
∵ ![]() ,
,
∴a2=( ![]() )2=2,即b2=1,
)2=2,即b2=1,
则椭圆的方程为 ![]() +y2=1
+y2=1
(2)解:设F1(﹣c,0),F2(c,0),
∵B(0,b),
∴直线BF2:y=﹣ ![]() x+b,代入椭圆方程
x+b,代入椭圆方程 ![]() +
+ ![]() =1(a>b>0)得(
=1(a>b>0)得( ![]() )x2﹣
)x2﹣ ![]() =0,
=0,
解得x=0,或x= ![]() ,
,
∵A( ![]() ,
, ![]() ),且A,C关于x轴对称,
),且A,C关于x轴对称,
∴C( ![]() ,﹣
,﹣ ![]() ),
),
则 ![]() =﹣
=﹣ ![]() =
= ![]() ,
,
∵F1C⊥AB,
∴ ![]() ×(
×( ![]() )=﹣1,
)=﹣1,
由b2=a2﹣c2得 ![]() ,
,
即e= ![]()
【解析】(1)根据椭圆的定义,建立方程关系即可求出a,b的值.(2)求出C的坐标,利用F1C⊥AB建立斜率之间的关系,解方程即可求出e的值.
【考点精析】本题主要考查了椭圆的标准方程的相关知识点,需要掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】己知在平面直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为 (
(![]() 为参数)以
为参数)以![]() 轴为极轴,
轴为极轴, ![]() 为极点建立极坐标系,在该极坐标系下,圆
为极点建立极坐标系,在该极坐标系下,圆![]() 是以点
是以点![]() 为圆心,且过点
为圆心,且过点![]() 的圆心.
的圆心.
(1)求圆![]() 及圆
及圆![]() 在平而直角坐标系
在平而直角坐标系![]() 下的直角坐标方程;
下的直角坐标方程;
(2)求圆![]() 上任一点
上任一点![]() 与圆
与圆![]() 上任一点之间距离的最小值.
上任一点之间距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)用五点作图法画出![]() 在长度为一个周期的区间上的图象;
在长度为一个周期的区间上的图象;

(2))求函数![]() 的单调递增区间;
的单调递增区间;
(3)简述如何由![]() 的图象经过适当的图象变换得到
的图象经过适当的图象变换得到![]() 的图象?
的图象?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 满足
满足![]() 且
且![]() ,则称函数
,则称函数![]() 为“
为“![]() 函数”.
函数”.
![]() 试判断
试判断![]() 是否为“
是否为“![]() 函数”,并说明理由;
函数”,并说明理由;
![]() 函数
函数![]() 为“
为“![]() 函数”,且当
函数”,且当![]() 时,
时,![]() ,求
,求![]() 的解析式,并写出在
的解析式,并写出在![]() 上的单调递增区间;
上的单调递增区间;
![]() 在
在![]() 条件下,当
条件下,当![]() 时,关于
时,关于![]() 的方程
的方程![]() 为常数
为常数![]() 有解,记该方程所有解的和为
有解,记该方程所有解的和为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某礼品店要制作一批长方体包装盒,材料是边长为![]() 的正方形纸板.如图所示,先在其中相邻两个角处各切去一个边长是
的正方形纸板.如图所示,先在其中相邻两个角处各切去一个边长是![]() 的正方形,然后在余下两个角处各切去一个长、宽分别为
的正方形,然后在余下两个角处各切去一个长、宽分别为![]() 、
、![]() 的矩形,再将剩余部分沿图中的虚线折起,做成一个有盖的长方体包装盒.
的矩形,再将剩余部分沿图中的虚线折起,做成一个有盖的长方体包装盒.

(1)求包装盒的容积![]() 关于
关于![]() 的函数表达式,并求函数的定义域;
的函数表达式,并求函数的定义域;
(2)当![]() 为多少时,包装盒的容积最大?最大容积是多少?
为多少时,包装盒的容积最大?最大容积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f (x)=ex,g(x)=x-b,b∈R.
(1)若函数f (x)的图象与函数g(x)的图象相切,求b的值;
(2)设T(x)=f (x)+ag(x),a∈R,求函数T(x)的单调增区间;
(3)设h(x)=|g(x)|·f (x),b<1.若存在x1,x2![]() [0,1],使|h(x1)-h(x2)|>1成立,求b的取值范围.
[0,1],使|h(x1)-h(x2)|>1成立,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙3人投篮,投进的概率分别是![]() .
.
(Ⅰ)现3人各投篮1次,求3人都没有投进的概率;
(Ⅱ)用![]() 表示乙投篮3次的进球数,求随机变量
表示乙投篮3次的进球数,求随机变量![]() 的概率分布及数学期望
的概率分布及数学期望![]() ;
;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙![]() 人投篮,投进的概率分别是
人投篮,投进的概率分别是![]() ,
,![]() ,
,![]() .
.
(1)现![]() 人各投篮
人各投篮![]() 次,求
次,求![]() 人至少一人投进的概率;
人至少一人投进的概率;
(2)用![]() 表示乙投篮
表示乙投篮![]() 次的进球数,求随机变量
次的进球数,求随机变量![]() 的概率分布及数学期望
的概率分布及数学期望![]() 和方差
和方差![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com