
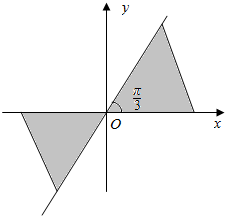
 如图所示,阴影部分表示的角的集合为(含边界){α|kπ≤α≤kπ+$\frac{π}{3}$,k∈Z}(用弧度表示).
如图所示,阴影部分表示的角的集合为(含边界){α|kπ≤α≤kπ+$\frac{π}{3}$,k∈Z}(用弧度表示). 分析 阴影部分表示的角α位于一、三象限,在第一象限,0≤α≤$\frac{π}{3}$;在第三象限,π≤α≤$\frac{4π}{3}$,由此能求出阴影部分表示的角的集合(含边界).
解答  解:如图,阴影部分表示的角α位于一、三象限,
解:如图,阴影部分表示的角α位于一、三象限,
在第一象限,0≤α≤$\frac{π}{3}$;在第三象限,π≤α≤$\frac{4π}{3}$,
∴阴影部分表示的角的集合为(含边界):
{α|2kπ≤α≤2kπ+$\frac{π}{3}$或(2k+1)π≤α≤(2k+1)π+$\frac{π}{3}$,k∈Z}={α|kπ≤α≤kπ+$\frac{π}{3}$,k∈Z}.
故答案为:{α|kπ≤α≤kπ+$\frac{π}{3}$,k∈Z}.
点评 本题表示角的集合的求法,是基础题,解题时要认真审题,注意终边相同的角的集合的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,已知直角梯形ABCO中,∠ABC=∠BCO=90°,AB=1,BC=$\sqrt{3}$,OA=OC=2,设$\overrightarrow{OM}$=m$\overrightarrow{OA}$,$\overrightarrow{ON}$=n$\overrightarrow{OC}$(其中0<m,n<1),G为线段MN的中点.
如图所示,已知直角梯形ABCO中,∠ABC=∠BCO=90°,AB=1,BC=$\sqrt{3}$,OA=OC=2,设$\overrightarrow{OM}$=m$\overrightarrow{OA}$,$\overrightarrow{ON}$=n$\overrightarrow{OC}$(其中0<m,n<1),G为线段MN的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com