
【题目】公元前![]() 世纪的毕达哥拉斯是最早研究“完全数”的人.完全数是一种特殊的自然数,它所有的真因子(即除了自身以外的约数)的和恰好等于它本身.若从集合
世纪的毕达哥拉斯是最早研究“完全数”的人.完全数是一种特殊的自然数,它所有的真因子(即除了自身以外的约数)的和恰好等于它本身.若从集合![]() 中随机抽取两个数,则这两个数中有完全数的概率是______.
中随机抽取两个数,则这两个数中有完全数的概率是______.
【答案】![]()
【解析】
依次按照完全数的定义1,6,24,28,36,得到集合![]() 中
中![]() 为完全数,
为完全数,![]() 不为完全数,在集合
不为完全数,在集合![]() 中任取两个数有
中任取两个数有![]() 种情况,在集合
种情况,在集合![]() 中任取两个数有
中任取两个数有![]() 种情况,利用古典概型和互斥事件的概率公式即得解.
种情况,利用古典概型和互斥事件的概率公式即得解.
1没有除自身外的约数,因此1不为完全数;
6的真因子为1,2,3,1+2+3=6,故6为完全数;
24的真因子为1,2,3,4,6,8,12,1+2+3+4+6+8+12=36,故24不为完全数;
28的真因子为1,2,4,7,14,1+2+4+7+14=28,故28为完全数;
36的真因子为1,2,3,4,6,9,12,18,1+2+3+4+6+9+12+18=54,故36不为完全数;
因此集合![]() 中
中![]() 为完全数,
为完全数,![]() 不为完全数.
不为完全数.
在集合![]() 中任取两个数有
中任取两个数有![]() 种情况;
种情况;
在集合![]() 中任取两个数有
中任取两个数有![]() 种情况;
种情况;
这两个数中有完全数的对立事件为取到的两个数都不是完全数,因此:![]()
故答案为:![]()


 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为
轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为![]() ,C1上任意一点P的直角坐标为
,C1上任意一点P的直角坐标为![]() ,通过变换
,通过变换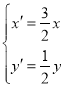 得到点P的对应点
得到点P的对应点![]() 的坐标.
的坐标.
(1)求点![]() 的轨迹C2的直角坐标方程;
的轨迹C2的直角坐标方程;
(2)直线![]() 的参数方程为
的参数方程为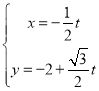 (
(![]() 为参数),
为参数),![]() 交C2于点M、N,点
交C2于点M、N,点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
支付方式 | (0,1000] | (1000,2000] | 大于2000 |
仅使用A | 18人 | 9人 | 3人 |
仅使用B | 10人 | 14人 | 1人 |
(Ⅰ)从全校学生中随机抽取1人,估计该学生上个月A,B两种支付方式都使用的概率;
(Ⅱ)从样本仅使用A和仅使用B的学生中各随机抽取1人,以X表示这2人中上个月支付金额大于1000元的人数,求X的分布列和数学期望;
(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用A的学生中,随机抽查3人,发现他们本月的支付金额都大于2000元.根据抽查结果,能否认为样本仅使用A的学生中本月支付金额大于2000元的人数有变化?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)是定义在R上的偶函数,且对任意的x∈R恒有f(x+1)=f(x﹣1),已知当x∈[0,1]时,f(x)=(![]() )1﹣x,则
)1﹣x,则
①2是函数f(x)的一个周期;
②函数f(x)在(1,2)上是减函数,在(2,3)上是增函数;
③函数f(x)的最大值是1,最小值是0;
④x=1是函数f(x)的一个对称轴;
⑤当x∈(3,4)时,f(x)=(![]() )x﹣3.
)x﹣3.
其中所有正确命题的序号是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线![]() 的参数方程为
的参数方程为![]() ,
,![]() 为参数
为参数![]() ,在以坐标原点为极点,x轴非负半轴为极轴的极坐标系中,曲线
,在以坐标原点为极点,x轴非负半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
![]() Ⅰ
Ⅰ![]() 写出
写出![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
![]() Ⅱ
Ⅱ![]() 若
若![]() 与
与![]() 相交于A,B两点,求
相交于A,B两点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 经过点
经过点![]() ,且与极轴所成的角为
,且与极轴所成的角为![]() .
.
(1)求曲线![]() 的普通方程及直线
的普通方程及直线![]() 的参数方程;
的参数方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的普通方程.
的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的两个焦点分别为
的两个焦点分别为![]() 和
和![]() ,短轴的两个端点分别为
,短轴的两个端点分别为![]() 和
和![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,且满足
上,且满足![]() ,当
,当![]() 变化时,给出下列三个命题:
变化时,给出下列三个命题:
①点![]() 的轨迹关于
的轨迹关于![]() 轴对称;②
轴对称;②![]() 的最小值为2;
的最小值为2;
③存在![]() 使得椭圆
使得椭圆![]() 上满足条件的点
上满足条件的点![]() 仅有两个,
仅有两个,
其中,所有正确命题的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1:![]() ,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C2是圆心极坐标为(3,π),半径为1的圆.
,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C2是圆心极坐标为(3,π),半径为1的圆.
(1)求曲线C1的参数方程和C2的直角坐标方程;
(2)设M,N分别为曲线C1,C2上的动点,求|MN|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|+|x+2|.
(1)若a=1.解不等式f(x)≤x2﹣1;
(2)若a>0,b>0,c>0.且f(x)的最小值为4﹣b﹣c.求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com