
| 到站时刻 | 8∶10 9∶10 | 8∶30 9∶30 | 8∶50 9∶50 |
| 概率 |  |  | 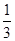 |
科目:高中数学 来源:不详 题型:解答题
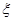 为与桌面接触的4个面上数字中偶数的个数,求
为与桌面接触的4个面上数字中偶数的个数,求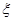 的分布列及期望E
的分布列及期望E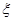 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 (
( )个大小相同的球,其中有3个红球和
)个大小相同的球,其中有3个红球和 个白球.已知从口袋中随机取出一个球是红球的概率是
个白球.已知从口袋中随机取出一个球是红球的概率是 .
.  时,不放回地从口袋中随机取出3个球,求取到白球的个数
时,不放回地从口袋中随机取出3个球,求取到白球的个数 的期望
的期望 ;
; ,有放回地从口袋中连续地取四次球(每次只取一个球),在四次摸球中恰好取到两次红球的概率大于
,有放回地从口袋中连续地取四次球(每次只取一个球),在四次摸球中恰好取到两次红球的概率大于 ,求
,求 和
和 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
甲部门不同岗位月工资 (元) (元) | 2200 | 2400 | 2600 | 2800 |
获得相应岗位的概率 | 0.4 | 0.3 | 0.2 | 0.1 |
乙部门不同岗位月工资 (元) (元) | 2000 | 2400 | 2800 | 3200 |
获得相应岗位的概率 | 0.4 | 0.3 | 0.2 | 0.1 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,指标甲、乙、丙检测合格分别记4分、2分、4分,若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响。
,指标甲、乙、丙检测合格分别记4分、2分、4分,若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响。 ,求
,求 的分布列与数学期望。
的分布列与数学期望。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
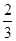 和
和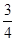 ,且各株大树是否成活互不影响.
,且各株大树是否成活互不影响. ,求
,求 分布列与期望.
分布列与期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
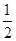 .若某人获得两个“支持”,则给予10万元的创业资助;若只获得一个“支持”,则给予5万元的资助;若未获得“支持”,则不予资助,令
.若某人获得两个“支持”,则给予10万元的创业资助;若只获得一个“支持”,则给予5万元的资助;若未获得“支持”,则不予资助,令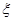 表示该公司的资助总额.
表示该公司的资助总额.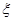 的分布列;
的分布列;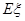 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com