
如图在三棱柱ABC-A1B1C1中,AB⊥AC,顶点A1在底面ABC上的射影恰为点B,且AB=AC=A1B=2.
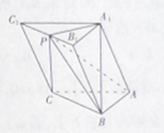
(1)证明:平面A1AC⊥平面AB1B;
(2)若点P为B1C1的中点,求三棱锥P-ABC与四棱锥P-AA1B1B的体积之比.
(1)证明详见解析;(2)1:1.
【解析】
试题分析:(1)根据直线与平面垂直的性质可得 ,而已知
,而已知 ,由直线与平面垂直的判定定理可得
,由直线与平面垂直的判定定理可得 面
面 ,根据平面与平面垂直的判定定理可得平面
,根据平面与平面垂直的判定定理可得平面 平面
平面 ;
;
(2)由已知可知, =2是三棱锥P ABC的高,△ABC是等腰直角三角形,可计算出求三棱锥P ABC的体积.由于AC⊥平面AB1B,点P为B1C1的中点,可知点P到平面
=2是三棱锥P ABC的高,△ABC是等腰直角三角形,可计算出求三棱锥P ABC的体积.由于AC⊥平面AB1B,点P为B1C1的中点,可知点P到平面 距离
距离 等于点
等于点 到平面
到平面 的距离的一半,计算出四棱锥P AA1B1B的体积即可求解.
的距离的一半,计算出四棱锥P AA1B1B的体积即可求解.
试题解析:证明:(1)由题意得: 平面ABC,
平面ABC,
∴ , 2分
, 2分
又 ,
,
∴AC垂直平面AB1B, 3分
∵ 面
面 ,∴平面
,∴平面 平面
平面 ; 5分
; 5分
(2)在三棱锥 中,因为
中,因为 ,
,
底面 是等腰直角三角形,
是等腰直角三角形,

又因为点P到底面的距离 =2,所以
=2,所以 . 6分
. 6分
由(1)可知AC⊥平面AB1B,
因为点P在B1C1的中点,
所以点P到平面AA1B1B距离h2等于点C1到平面AA1B1B的距离的一半,即h2=1. 8分
 , 10分
, 10分
所以三棱锥P ABC与四棱锥P AA1B1A1的体积之比为1:1. 12分
考点:1.直线与平面垂直的性质;2.平面与平面垂直的判断和性质;3.锥体的体积.


科目:高中数学 来源:2013-2014学年河北省高三第一次模拟考试理科数学试卷(解析版) 题型:填空题
在 轴的正方向上,从左向右依次取点列
轴的正方向上,从左向右依次取点列  ,以及在第一象限内的抛物线
,以及在第一象限内的抛物线 上从左向右依次取点列
上从左向右依次取点列 ,使
,使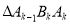 (
(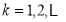 )都是等边三角形,其中
)都是等边三角形,其中 是坐标原点,则第2005个等边三角形的边长是 .
是坐标原点,则第2005个等边三角形的边长是 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省石家庄市毕业班第一次模拟考试数学理科数学试卷(解析版) 题型:解答题
在直角坐标系中,曲线C1的参数方程为: (
( 为参数),以原点为极点,x轴的正半轴为极轴,并取与直角坐标系相同的长度单位,建立极坐标系,曲线C2是极坐标方程为:
为参数),以原点为极点,x轴的正半轴为极轴,并取与直角坐标系相同的长度单位,建立极坐标系,曲线C2是极坐标方程为: ,
,
(1)求曲线C2的直角坐标方程;
(2)若P,Q分别是曲线C1和C2上的任意一点,求 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省石家庄市毕业班第一次模拟考试数学理科数学试卷(解析版) 题型:选择题
执行如图所示的程序框图,若输出的结果为3,则可输入的实数x值的个数为( )
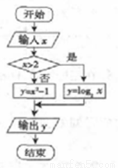
A.1 B.2 C.4 D.3
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省石家庄市毕业班第一次模拟考试数学理文数学试卷(解析版) 题型:解答题
在直角坐标系中,曲线C1的参数方程为: (
( 为参数),以原点为极点,x轴的正半轴为极轴,并取与直角坐标系相同的长度单位,建立极坐标系,曲线C2是极坐标方程为:
为参数),以原点为极点,x轴的正半轴为极轴,并取与直角坐标系相同的长度单位,建立极坐标系,曲线C2是极坐标方程为: ,
,
(1)求曲线C2的直角坐标方程;
(2)若P,Q分别是曲线C1和C2上的任意一点,求 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省石家庄市毕业班第一次模拟考试数学理文数学试卷(解析版) 题型:选择题
已知等差数列{an},且3(a3+a5)+2(a7+a10+a13)=48,则数列{an}的前13项之和为()
A.24
B.39
C.104
D.52
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省唐山市高三年级第二次模拟考试理科数学试卷(解析版) 题型:填空题
商场经营的某种袋装大米质量(单位:kg)服从正态分布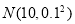 ,任取一袋大米,质量不足9.8kg的概率为 .(精确到0.0001)
,任取一袋大米,质量不足9.8kg的概率为 .(精确到0.0001)
注: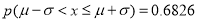 ,
,
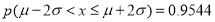 ,
,
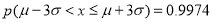
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省唐山市高三年级第三次模拟考试理科数学试卷(解析版) 题型:解答题
过抛物线C: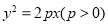 上的点M分别向C的准线和x轴作垂线,两条垂线及C的准线和x轴围成边长为4的正方形,点M在第一象限.
上的点M分别向C的准线和x轴作垂线,两条垂线及C的准线和x轴围成边长为4的正方形,点M在第一象限.
(1)求抛物线C的方程及点M的坐标;
(2)过点M作倾斜角互补的两条直线分别与抛物线C交于A,B两点,如果点M在直线AB的上方,求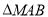 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com