
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,焦距为2,且经过点
,焦距为2,且经过点![]() ,斜率为
,斜率为![]() 的直线
的直线![]() 经过点
经过点![]() ,与椭圆
,与椭圆![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)在![]() 轴上是否存在点
轴上是否存在点![]() ,使得以
,使得以![]() ,
,![]() 为邻边的平行四边形是菱形?如果存在,求出
为邻边的平行四边形是菱形?如果存在,求出![]() 的取值范围,如果不存在,请说明理由.
的取值范围,如果不存在,请说明理由.
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:
【题目】第七届世界军人运动会于2019年10月18日至27日在中国武汉举行,中国队以133金64银42铜位居金牌榜和奖牌榜的首位.运动会期间有甲、乙等五名志愿者被分配到射击、田径、篮球、游泳四个运动场地提供服务,要求每个人都要被派出去提供服务,且每个场地都要有志愿者服务,则甲和乙恰好在同一组的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,四边形![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一点,满足
上一点,满足![]() ,
,![]() 为
为![]() 的中点,现将梯形沿
的中点,现将梯形沿![]() 折叠(如图2),使平面
折叠(如图2),使平面![]() 平面
平面![]() .
.
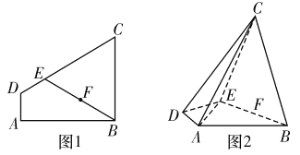
(1)求证:平面![]() 平面
平面![]() ;
;
(2)能否在线段![]() 上找到一点
上找到一点![]() (端点除外)使得直线
(端点除外)使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ?若存在,试确定点
?若存在,试确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项等比数列{an}满足a1=2,2a2=a4﹣a3,数列{bn}满足bn=1+2log2an.
(1)求数列{an},{bn}的通项公式;
(2)令cn=anbn,求数列{cn}的前n项和Sn;
(3)若λ>0,且对所有的正整数n都有2λ2﹣kλ+2![]() 成立,求k的取值范围.
成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的几何体B-ACDE中,AB⊥AC,AB=4,AC=3,DC⊥平面ABC,EA⊥平面ABC,点M在线段BC上,且AM=![]() .
.
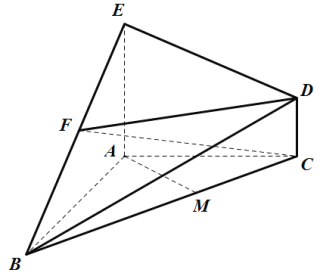
(1)证明:AM⊥平面BCD;
(2)若点F为线段BE的中点,且三棱锥F-BCD的体积为1,求CD的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的各项均为正数,记数列
的各项均为正数,记数列![]() 的前n项和为
的前n项和为![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]() .
.
(1)求![]() 的值;
的值;
(2)求数列![]() 的通项公式;
的通项公式;
(3)若![]() ,且
,且![]() 成等比数列,求k和t的值.
成等比数列,求k和t的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() 为直线
为直线![]() 的倾斜角),以坐标原点
的倾斜角),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的直角坐标方程,并求
的直角坐标方程,并求![]() 时直线
时直线![]() 的普通方程;
的普通方程;
(2)直线![]() 和曲线
和曲线![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 的直角坐标为
的直角坐标为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)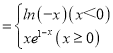 ,若关于x的方程f2(x)﹣af(x)+a﹣a2=0有四个不等的实数根,则a的取值范围是( )
,若关于x的方程f2(x)﹣af(x)+a﹣a2=0有四个不等的实数根,则a的取值范围是( )
A.![]() B.(﹣∞,﹣1)∪[1,+∞)
B.(﹣∞,﹣1)∪[1,+∞)
C.(﹣∞,﹣1)∪{1}D.(﹣1,0)∪{1}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com