
【题目】已知椭圆C: ![]() ,左焦点
,左焦点 ![]() ,且离心率
,且离心率 ![]() (Ⅰ)求椭圆C的方程;
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l:y=kx+m(k≠0)与椭圆C交于不同的两点M,N(M,N不是左、右顶点),且以MN为直径的圆经过椭圆C的右顶点A.求证:直线l过定点,并求出定点的坐标.
【答案】(Ⅰ)解:∵椭圆C: ![]() , 左焦点
, 左焦点 ![]() ,且离心率
,且离心率 ![]() ,
,
∴c= ![]() ,
, ![]() ,
,
∴a=2,b2=4﹣3=1,
∴椭圆C的方程 ![]() .
.
(Ⅱ)证明:设M(x1 , y1) N(x2 , y2),
右顶点A(2,0)![]() ,
,
∵以MN为直径的圆经过椭圆C的右顶点A,
∴(2﹣x2)(2﹣x1)+y1y2=0,
∵y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2
∴4+(km﹣2)(x1+x2)+(1+k2)x1x2+m2=0 ①
把y=kx+m代入椭圆方程 ![]() ,
,
得 ![]() +(kx+m)2=1,
+(kx+m)2=1,
整理,得( ![]() +k2)x2+2kmx+m2﹣1=0,
+k2)x2+2kmx+m2﹣1=0,
所以x1x2= ![]() ,x1+x2=﹣
,x1+x2=﹣ ![]() ,②
,②
把②入①,得
4+(km﹣2)(﹣ ![]() )+(1+k2)
)+(1+k2) ![]() +m2
+m2
=(5m2+16km+12k2)÷(1+4k2)
=(m+2k)(5m+6k)÷(1+4k2)
=0
所以m+2k=0 或者 m+ ![]() k=0
k=0
当m+2k=0时,直线y=kx﹣2k恒过点(2,0)和A点重合显然不符合
当m+ ![]() k=0时 直线恒过点(
k=0时 直线恒过点( ![]() ,0)符合题意
,0)符合题意
所以该定点坐标就是( ![]() ,0)
,0)
【解析】(I)由题设知c= ![]() ,
, ![]() ,由此能求出椭圆C的方程.(II)设M(x1 , y1) N(x2 , y2),右顶点A(2,0),
,由此能求出椭圆C的方程.(II)设M(x1 , y1) N(x2 , y2),右顶点A(2,0), ![]() ,由以MN为直径的圆经过椭圆C的右顶点A,知(2﹣x2)(2﹣x1)+y1y2=0,由y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2 , 知4+(km﹣2)(x1+x2)+(1+k2)x1x2+m2=0.把y=kx+m代入椭圆方程
,由以MN为直径的圆经过椭圆C的右顶点A,知(2﹣x2)(2﹣x1)+y1y2=0,由y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2 , 知4+(km﹣2)(x1+x2)+(1+k2)x1x2+m2=0.把y=kx+m代入椭圆方程 ![]() ,得(
,得( ![]() +k2)x2+2kmx+m2﹣1=0,再由韦达定理结合题设条件能求出该定点坐标.
+k2)x2+2kmx+m2﹣1=0,再由韦达定理结合题设条件能求出该定点坐标.
【考点精析】本题主要考查了椭圆的标准方程的相关知识点,需要掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 才能正确解答此题.
才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知定点F(1,0),动点P(异于原点)在y轴上运动,连接FP,过点P作PM交x轴于点M,并延长MP到点N,且 ![]() ,
, ![]() .
.
(1)求动点N的轨迹C的方程;
(2)若直线l与动点N的轨迹交于A、B两点,若 ![]() 且
且 ![]() ,求直线l的斜率k的取值范围.
,求直线l的斜率k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)为定义在R上的奇函数,且当x≥0时,f(x)=x2﹣(a+4)x+a.
(1)求实数a的值及f(x)的解析式;
(2)求使得f(x)=x+6成立的x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是正方体的平面展开图,在这个正方体中, ①BM与ED平行;
②CN与BE是异面直线;
③CN与BM成60°角;
④DM与BN垂直.
以上四个命题中,正确命题的序号是( )
A.③
B.③④
C.①③
D.①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一个几何体的三视图及其尺寸(单位:cm),则该几何体的表面积和体积分别为( ) 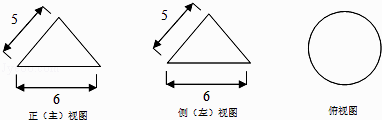
A.24πcm2 , 12πcm3
B.15πcm2 , 12πcm3
C.24πcm2 , 36πcm3
D.15πcm2 , 36πcm3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆C: ![]() +
+ ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,其左焦点到点P(2,1)的距离为
,其左焦点到点P(2,1)的距离为 ![]() . (Ⅰ)求椭圆C的标准方程;
. (Ⅰ)求椭圆C的标准方程;
(Ⅱ)若直线l:y=kx+m与椭圆C相交于A,B两点(A,B不是左右顶点),且以AB为直径的圆过椭圆C的右顶点.求证:直线l过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AB=1,AC=2,BC= ![]() ,D,E分别是AC1和BB1的中点,则直线DE与平面BB1C1C所成的角为( )
,D,E分别是AC1和BB1的中点,则直线DE与平面BB1C1C所成的角为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的中心在原点,焦点在x轴上,离心率为 ![]() ,且经过点M(4,1),直线l:y=x+m交椭圆于不同的两点A,B. (Ⅰ)求椭圆的方程;
,且经过点M(4,1),直线l:y=x+m交椭圆于不同的两点A,B. (Ⅰ)求椭圆的方程;
(Ⅱ)求m的取值范围;
(Ⅲ)若直线l不过点M,求证:直线MA、MB与x轴围成一个等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com