
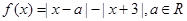 .
.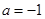 时,解不等式
时,解不等式 ;
; 时,
时,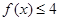 ,求a的取值范围.
,求a的取值范围. ;(2)[-7,7].
;(2)[-7,7]. 的解析式,利用零点分段法去掉绝对值,解不等式组,得到不等式的解集;第二问,在已知的
的解析式,利用零点分段法去掉绝对值,解不等式组,得到不等式的解集;第二问,在已知的 范围内
范围内 的绝对值可去掉,解绝对值不等式,使之转化成2个恒成立.
的绝对值可去掉,解绝对值不等式,使之转化成2个恒成立. ;
; . 5分
. 5分

 备战中考寒假系列答案
备战中考寒假系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com