
【题目】如图,锐角△ABC中, ![]() =
= ![]() ,
, ![]() =
= ![]() ,点M为BC的中点. (Ⅰ)试用
,点M为BC的中点. (Ⅰ)试用 ![]() ,
, ![]() 表示
表示 ![]() ;
;
(Ⅱ)若| ![]() |=5,|
|=5,| ![]() |=3,sin∠BAC=
|=3,sin∠BAC= ![]() ,求中线AM的长.
,求中线AM的长.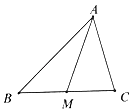
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() 的离心率为
的离心率为![]() ,其左焦点到点
,其左焦点到点![]() 的距离为
的距离为![]() .不过原点
.不过原点![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() 两点,且线段
两点,且线段![]() 被直线
被直线![]() 平分.
平分.
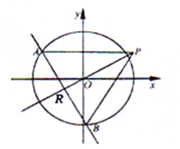
(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 的面积取最大值时直线
的面积取最大值时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中有五张卡片,其中红色卡片三张,标号分别为1,2,3;蓝色卡片两张,标号分别为1,2.
(1)从以上五张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率;
(2)现袋中再放入一张标号为0的绿色卡片,从这六张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于两个图形F1 , F2 , 我们将图象F1上任意一点与图形F2上的任意一点间的距离中的最小值,叫作图形F1与F2图形的距离,若两个函数图象的距离小于1,则这两个函数互为“可及函数”,给出下列几对函数,其中互为“可及函数”的是 . (写出所有正确命题的编号) ①f(x)=cosx,g(x)=2;
②f(x)=ex . g(x)=x;
③f(x)=log2(x2﹣2x+5),g(x)=sin ![]() ﹣x;
﹣x;
④f(x)=x+ ![]() ,g(x)=lnx+2.
,g(x)=lnx+2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名高三学生的课外体育锻炼平均每天运动的时间进行调查,如表:(平均每天锻炼的时间单位:分钟)
平均每天锻炼 | [0,10) | [10,20) | [20,30) | [30,40) | [40,50) | [50,60) |
总人数 | 20 | 36 | 44 | 50 | 40 | 10 |
将学生日均课外课外体育运动时间在[40,60)上的学生评价为“课外体育达标”.
(1)请根据上述表格中的统计数据填写下面2×2列联表,并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关?
课外体育不达标 | 课外体育达标 | 合计 | |
男 | |||
女 | 20 | 110 | |
合计 |
(2)将上述调查所得到的频率视为概率.现在从该校高三学生中,抽取3名学生,记被抽取的3名学生中的“课外体育达标”学生人数为X,若每次抽取的结果是相互独立的,求X的数学期望和方差.
参考公式: ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
参考数据:
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以原点为圆心,单位长度为半径的圆上有两点A( ![]() ,
, ![]() ),B(
),B( ![]() ,
, ![]() ). (Ⅰ)求
). (Ⅰ)求 ![]() ,
, ![]() 夹角的余弦值;
夹角的余弦值;
(Ⅱ)已知C(1,0),记∠AOC=α,∠BOC=β,求tan ![]() 的值.
的值.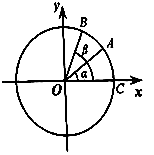
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com