
分析 (Ⅰ)利用奇函数的定义判断双曲正弦函数的奇偶性;
(Ⅱ)对选项分别进行判断,即可得出结论;
(Ⅲ)(Ⅲ)y=tanhx=$\frac{sinhx}{coshx}$,e2x=$\frac{1+tanhx}{1-tanhx}$,即可得出结论.
解答 解:(Ⅰ)∵sin(-hx)=$\frac{{e}^{-x}-{e}^{x}}{2}$=-sinhx,
∴双曲正弦函数是奇函数;
(Ⅱ)①sinh2x+cosh2x=$\frac{{e}^{2x}+{e}^{-2x}-2}{4}$+$\frac{{e}^{2x}+{e}^{-2x}+2}{4}$≠1,不正确;
②sinh2x═$\frac{{e}^{2x}-{e}^{-2x}}{2}$=2sinhx•coshy,正确;
③cosh2x-sinh2x=$\frac{{e}^{2x}+{e}^{-2x}+2}{4}$-$\frac{{e}^{2x}+{e}^{-2x}-2}{4}$≠cosh2x,不正确.
(Ⅲ)y=tanhx=$\frac{sinhx}{coshx}$,∴e2x=$\frac{1+tanhx}{1-tanhx}$
tanh2x=$\frac{sinh2x}{cosh2x}$=$\frac{{e}^{2x}-{e}^{-2x}}{{e}^{2x}+{e}^{-2x}}$=-$\frac{2tanhx}{1+tan{h}^{2}x}$.
故答案为:②.
点评 本题为开放题型,考查类比推理,考查分析问题、解决问题的能力.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (1-a)a>(1+a)a | B. | log1-a(1+a)<0 | C. | (1-a)1+a>1 | D. | ${(1-a)}^{\frac{1}{a}}$>1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{11}{8}$ | B. | $\frac{13}{8}$ | C. | $\frac{8}{11}$ | D. | $\frac{8}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,△PBD是直角三角形,∠PDB=90°,以BA为直径作⊙O,设点C是圆⊙O与直线PD的公共点,若∠ABC=∠DBC.
如图,△PBD是直角三角形,∠PDB=90°,以BA为直径作⊙O,设点C是圆⊙O与直线PD的公共点,若∠ABC=∠DBC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
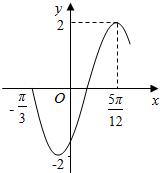 函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则这个函数的周期和初相分别是( )
函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则这个函数的周期和初相分别是( )| A. | 2,-$\frac{π}{3}$ | B. | 2,-$\frac{π}{6}$ | C. | π,-$\frac{π}{6}$ | D. | π,-$\frac{π}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com