
【题目】甲、乙两人在相同条件下各射击![]() 次,每次中靶环数情况如图所示:
次,每次中靶环数情况如图所示:
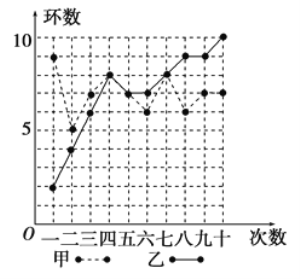
(1)请填写下表(先写出计算过程再填表):
平均数 | 方差 | 命中 | |
甲 |
|
|
|
乙 |
(2)从下列三个不同的角度对这次测试结果进行
①从平均数和方差相结合看(分析谁的成绩更稳定);
②从平均数和命中![]() 环及
环及![]() 环以上的次数相结合看(分析谁的成绩好些);
环以上的次数相结合看(分析谁的成绩好些);
③从折线图上两人射击命中环数的走势看(分析谁更有潜力).
【答案】(1)填表见解析;(2)①甲成绩比乙稳定;②乙成绩比甲好些;③乙更有潜力.
【解析】
(1)由拆线图,求出![]() 和
和![]() ,完成列联表.
,完成列联表.
(2)①平均数相同,![]() ,从而甲成绩比乙稳定.
,从而甲成绩比乙稳定.
②平均数相同,命中9环及9环以上的次数甲比乙少,乙成绩比甲好些.
③甲成绩在平均数上下波动;而乙处于上升势头,从第三次以后就没有比甲少的情况发生,乙更有潜力.
解:由列联表中数据,计算由题图,知:
甲射击10次中靶环数分别为9,5,7,8,7,6,8,6,7,7.
将它们由小到大排列为5,6,6,7,7,7,7,8,8,9.
乙射击10次中靶环数分别为2,4,6,8,7,7,8,9,9,10.
将它们由小到大排列为2,4,6,7,7,8,8,9,9,10.
(1)![]() (环
(环![]() ,
,
![]() .
.
填表如下:
平均数 | 方差 | 命中9环及9环以上的次数 | |
甲 | 7 | 1.2 | 1 |
乙 | 7 | 5.4 | 3 |
(2)①![]() 平均数相同,
平均数相同,![]() ,
,![]() 甲成绩比乙稳定.
甲成绩比乙稳定.
②![]() 平均数相同,命中9环及9环以上的次数甲比乙少,
平均数相同,命中9环及9环以上的次数甲比乙少,![]() 乙成绩比甲好些.
乙成绩比甲好些.
③甲成绩在平均数上下波动;而乙处于上升势头,从第三次以后就没有比甲少的情况发生,乙更有潜力.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:
【题目】某医疗器械公司在全国共有![]() 个销售点,总公司每年会根据每个销售点的年销量进行评价分析.规定每个销售点的年销售任务为一万四千台器械.根据这
个销售点,总公司每年会根据每个销售点的年销量进行评价分析.规定每个销售点的年销售任务为一万四千台器械.根据这![]() 个销售点的年销量绘制出如下的频率分布直方图.
个销售点的年销量绘制出如下的频率分布直方图.
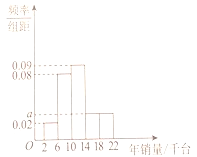
(1)完成年销售任务的销售点有多少个?
(2)若用分层抽样的方法从这![]() 个销售点中抽取容量为
个销售点中抽取容量为![]() 的样本,求该五组
的样本,求该五组![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,(单位:千台)中每组分别应抽取的销售点数量.
,(单位:千台)中每组分别应抽取的销售点数量.
(3)在(2)的条件下,从该样本中完成年销售任务的销售点中随机选取![]() 个,求这两个销售点不在同一组的概率.
个,求这两个销售点不在同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况.下列叙述中正确的是( )
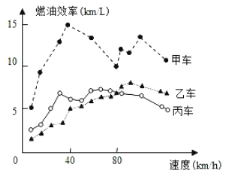
A.消耗1升汽油,乙车最多可行驶5千米
B.以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C.甲车以80千米/小时的速度行驶1小时,消耗8升汽油
D.某城市机动车最高限速80千米/小时.相同条件下,在该市用乙车比用丙车更省油
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知点
中,已知点![]() ,圆
,圆![]() :
:![]() 与
与![]() 轴的正半轴的交点是
轴的正半轴的交点是![]() ,过点
,过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() .
.

(1)若直线![]() 与
与![]() 轴交于
轴交于![]() ,且
,且![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)设直线![]() ,
,![]() 的斜率分别是
的斜率分别是![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)设![]() 的中点为
的中点为![]() ,点
,点![]() ,若
,若![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1, ![]() ,其中n∈N*.
,其中n∈N*.
(1)设![]() ,求证:数列{bn}是等差数列,并求出{an}的通项公式.
,求证:数列{bn}是等差数列,并求出{an}的通项公式.
(2)设![]() ,数列{cncn+2}的前n项和为Tn,是否存在正整数m,使得
,数列{cncn+2}的前n项和为Tn,是否存在正整数m,使得![]() 对于n∈N*,恒成立?若存在,求出m的最小值;若不存在,请说明.
对于n∈N*,恒成立?若存在,求出m的最小值;若不存在,请说明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,共享单车已经悄然进入了广大市民的日常生活,并慢慢改变了人们的出行方式.为了更好地服务民众,某共享单车公司在其官方![]() 中设置了用户评价反馈系统,以了解用户对车辆状况和优惠活动的评价.现从评价系统中选出
中设置了用户评价反馈系统,以了解用户对车辆状况和优惠活动的评价.现从评价系统中选出![]() 条较为详细的评价信息进行统计,车辆状况的优惠活动评价的
条较为详细的评价信息进行统计,车辆状况的优惠活动评价的![]() 列联表如下:
列联表如下:
对优惠活动好评 | 对优惠活动不满意 | 合计 | |
对车辆状况好评 |
|
|
|
对车辆状况不满意 |
|
|
|
合计 |
|
|
|
(1)能否在犯错误的概率不超过![]() 的前提下认为优惠活动好评与车辆状况好评之间有关系?
的前提下认为优惠活动好评与车辆状况好评之间有关系?
(2)为了回馈用户,公司通过![]() 向用户随机派送骑行券.用户可以将骑行券用于骑行付费,也可以通过
向用户随机派送骑行券.用户可以将骑行券用于骑行付费,也可以通过![]() 转赠给好友.某用户共获得了
转赠给好友.某用户共获得了![]() 张骑行券,其中只有
张骑行券,其中只有![]() 张是一元券.现该用户从这
张是一元券.现该用户从这![]() 张骑行券中随机选取
张骑行券中随机选取![]() 张转赠给好友,求选取的
张转赠给好友,求选取的![]() 张中至少有
张中至少有![]() 张是一元券的概率.
张是一元券的概率.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com