
直线l:y=kx+1与双曲线C:2x2-y2=1的右支交于不同的两点A、B.
(1)求实数k的取值范围;
(2)是否存在实数k,使得以线段AB为直径的圆经过双曲线C的右焦点F?若存在,求出k的值;若不存在,说明理由.
(1)k的取值范围为-2<k<-![]() (2)k=-
(2)k=-![]() 使得以线段AB为直径的圆经过双曲线C的右焦点
使得以线段AB为直径的圆经过双曲线C的右焦点
(1)将直线l的方程y=kx+1代入双曲线C的方程2x2-y2=1后,整理得(k2-2)x2+2kx+2=0 ①
依题意,直线l与双曲线C的右支交于不同两点,
故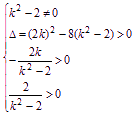
解得k的取值范围为-2<k<-![]() .
.
(2)设A、B两点的坐标分别为(x1,y1),(x2,y2),
则由①式得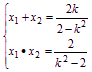 ②
②
假设存在实数k,使得以线段AB为直径的圆经过双曲线C的右焦点F(c,0),则由FA⊥FB得
(x1-c)(x2-c)+y1y2=0.
即(x1-c)(x2-c)+(kx1+1)(kx2+1)=0.
整理得:
(k2+1)x1x2+(k-c)(x1+x2)+c2+1=0 ③
把②式及c=![]() 代入③式化简得
代入③式化简得
5k2+2![]() k-6=0.
k-6=0.
解得k=-![]() 或k=
或k=![]()
![]() (-2,-
(-2,-![]() )(舍去).
)(舍去).
可知k=-![]() 使得以线段AB为直径的圆经过双曲线C的右焦点.
使得以线段AB为直径的圆经过双曲线C的右焦点.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:
(1)求实数k的取值范围;
(2)是否存在实数k,使得以线段AB为直径的圆经过双曲线C的右焦点F?若存在,求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
A.(-∞,-1) B.(-∞,-1] C.(1,+∞) D.[1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
(Ⅰ)求实数k的取值范围;
(Ⅱ)是否存在实数k,使得以线段AB为直径的圆经过双曲线C的右焦点F?若存在,求出k的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
直线l:y=kx+1与双曲线C:2x2-y2=1的右支交于不同的两点A、B.
(1)求实数k的取值范围.
(2)是否存在实数k,使得以线段AB为直径的圆经过双曲线C的右焦点F2?若存在,求出k的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com