
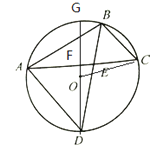
【题目】如图,圆O为△ABC的外接圆,D为![]() 的中点,BD交AC于E.
的中点,BD交AC于E.
(Ⅰ)证明:AD2=DEDB;
(Ⅱ)若AD∥BC,DE=2EB,AD=![]() , 求圆O的半径.
, 求圆O的半径.
【答案】证明:(Ⅰ)连接OD,OC,
∵D是弧AC的中点,∴∠ABD=∠CBD
∵∠ABD=∠ECD∴∠CBD=∠ECD
∵∠BDA=∠EDA∴△BAD∽△AED
∴![]() ,
,
∴AD2=DEDB.
解:(2)∵D是弧AC的中点,∴OD⊥AC,
∵AD∥BC,DE=2EB,AD=![]() ,△BEC∽△AED,∴BC=
,△BEC∽△AED,∴BC=![]() ,
,
∴∠ACB=∠DAC,∠BDC=∠ADB,
∵∠ADB=∠ACB,∠DAC=∠DBC,∴BE=CE,AE=DE,
延长DO交AC于F,交圆于G,
设BE=x,则DE=2x,
∵AD2=DEDB,∴6=2x3x,解得BE=CE=1,DE=AE=2,
∴AF=CF=![]() ,DF=
,DF=![]() =
=![]() ,
,
设圆半径为r,则 OC=r,
∴r2=(![]() ﹣r)2+(
﹣r)2+(![]() )2 , 解得r=
)2 , 解得r=![]() .
.
∴圆半径为![]() .
.
【解析】(Ⅰ)连接OD,OC,推导出△BAD∽△AED,由此能证明AD2=DEDB.
(2)设⊙O的半径为r,推导出△BEC∽△AED,从而求出BE=CE=1,DE=AE=2,由此能求出圆半径.


科目:高中数学 来源: 题型:
【题目】给出下列四个结论:
①当a为任意实数时,直线(a﹣1)x﹣y+2a+1=0恒过定点P,则过点P且焦点在y轴上的抛物线的标准方程是![]() ;
;
②已知双曲线的右焦点为(5,0),一条渐近线方程为2x﹣y=0,则双曲线的标准方程是![]() ;
;
③抛物线![]() 的准线方程为
的准线方程为![]() .
.
④已知双曲线![]() ,其离心率e∈(1,2),则m的取值范围是(﹣12,0).
,其离心率e∈(1,2),则m的取值范围是(﹣12,0).
其中正确命题的序号是___________.(把你认为正确命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别是△ABC的内角A,B,C的对边,若△ABC的周长为2(![]() +1),且sin B+sin C=
+1),且sin B+sin C=![]() sin A,则a= ( )
sin A,则a= ( )
A. ![]() B. 2 C. 4 D.
B. 2 C. 4 D. ![]()
【答案】B
【解析】
根据正弦定理把![]() 转化为边的关系,进而根据△ABC的周长,联立方程组,可求出a的值.
转化为边的关系,进而根据△ABC的周长,联立方程组,可求出a的值.
根据正弦定理,![]() 可化为
可化为![]()
∵△ABC的周长为![]() ,
,
∴联立方程组![]() ,
,
解得a=2.
故选:B
【点睛】
(1)在三角形中根据已知条件求未知的边或角时,要灵活选择正弦、余弦定理进行边角之间的转化,以达到求解的目的.
(2)求角的大小时,在得到角的某一个三角函数值后,还要根据角的范围才能确定角的大小,这点容易被忽视,解题时要注意.
【题型】单选题
【结束】
7
【题目】已知数列{an}中,an=n2-kn(n∈N*),且{an}单调递增,则k的取值范围是( )
A. (-∞,2] B. (-∞,2) C. (-∞,3] D. (-∞,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,A=120°,AB=5,BC=![]() ,则AC的值为________.
,则AC的值为________.
【答案】2
【解析】
利用余弦定理可得关于AC的方程,解之即可.
由余弦定理可知cosA=![]() =
=![]() =﹣
=﹣![]() ,
,
解得AC=2或﹣7(舍去)
故答案为:2
【点睛】
对于余弦定理一定要熟记两种形式:(1)![]() ;(2)
;(2)![]() .另外,在解与三角形、三角函数有关的问题时,还要记住
.另外,在解与三角形、三角函数有关的问题时,还要记住![]() ,
, ![]() ,
, ![]() 等特殊角的三角函数值,以便在解题中直接应用.
等特殊角的三角函数值,以便在解题中直接应用.
【题型】填空题
【结束】
15
【题目】“嫦娥奔月,举国欢庆”,据科学计算,运载“神六”的“长征二号”系列火箭,在点火第一秒钟通过的路程为2 km,以后每秒钟通过的路程都增加2 km,在达到离地面210 km的高度时,火箭与飞船分离,则这一过程大约需要的时间是______秒.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数y=![]() sin4x﹣
sin4x﹣![]() cos4x的图象,可以将函数y=sin4x的图象( )
cos4x的图象,可以将函数y=sin4x的图象( )
A.向右平移![]() 个单位
个单位
B.向左平移![]() 个单位
个单位
C.向右平移![]() 个单位
个单位
D.向左平移![]() 个单位
个单位
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com