已知圆C的方程为:(x+1)2+(y-2)2=2.
(1)过原点斜率为k的直线与圆C相交于A、B两点,若|AB|=2,求k的值;
(2)若圆C的切线l在x轴和y轴上的截距相等,求切线l的方程.
【答案】
分析:由圆C的方程找出圆心C的坐标和半径r,
(1)由直线过原点且斜率为k,设出直线的方程为y=kx,利用点到直线的距离公式表示出圆心C到直线的距离d,由已知|AB|的长,以及圆的半径r,利用垂径定理及勾股定理求出圆心C到直线的距离d,可列出关于k的方程,求出方程的解即可得到k的值;
(2)分两种情况考虑:①当切线l过原点时,设切线l的方程为y=kx,利用点到直线的距离公式求出圆心C到切线l的距离d,根据直线与圆相切时圆心到直线的距离d=r,列出关于k的方程,求出方程的解即可确定出此时切线l的方程;②当切线l不过原点时,设切线l的方程为x+y-a=0,根据d=r,利用点到直线的距离公式列出关于a的方程,求出方程的解得到a的值,确定出此时切线的方程,综上,得到所有满足题意的切线l的方程.
解答:解:由圆的方程(x+1)
2+(y-2)
2=2,得到圆心C的坐标为(-1,2),半径r=
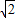
,
(1)设直线的方程为y=kx,即kx-y=0,
∵r=
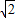
,|AB|=2,
∴圆心C到直线的距离d=
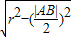
=1,又d=
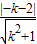
,
∴
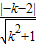
=1,即(k+2)
2=k
2+1,
解得:k=-

;
(2)分两种情况考虑:
①若切线l过原点,设l方程为y=kx,即kx-y=0,
则由C(-1,2)到l的距离d=
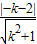
=r=

,即(k+2)
2=2k
2+2,
解得:k=2±

,
∴此时切线l的方程为y=(2±
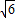
)x;
②若切线l不过原点,设l的方程为x+y-a=0,
则由C(-1,2)到l的距离d=
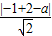
=r=
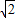
,即|a-1|=2,
可得a-1=2或a-1=-2,解得:a=3或a=-1,
∴此时切线方程为x+y-3=0或x+y+1=0,
综上,切线l的方程为y=(2±
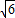
)x或x+y-3=0或x+y+1=0.
点评:此题考查了直线与圆相交的性质,以及直线的截距式方程,涉及的知识有:垂径定理,勾股定理,圆的标准方程,点到直线的距离公式,当直线与圆相交时,常常根据垂径定理由垂直得中点,进而由弦长的一半,圆的半径及弦心距构造直角三角形,利用勾股定理来解决问题;当直线与圆相切时,圆心到直线的距离等于圆的半径,即d=r,熟练掌握此性质是解本题第二问的关键.

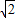 ,
,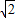 ,|AB|=2,
,|AB|=2,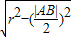 =1,又d=
=1,又d=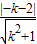 ,
,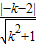 =1,即(k+2)2=k2+1,
=1,即(k+2)2=k2+1, ;
;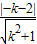 =r=
=r= ,即(k+2)2=2k2+2,
,即(k+2)2=2k2+2, ,
,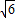 )x;
)x;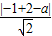 =r=
=r=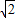 ,即|a-1|=2,
,即|a-1|=2,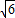 )x或x+y-3=0或x+y+1=0.
)x或x+y-3=0或x+y+1=0.

 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案 如图,已知圆C的方程为:x2+y2+x-6y+m=0,直线l的方程为:x+2y-3=0.
如图,已知圆C的方程为:x2+y2+x-6y+m=0,直线l的方程为:x+2y-3=0.