
 )](x-4)<0,其中a+
)](x-4)<0,其中a+ <0,故解集为(a+
<0,故解集为(a+ ,4),利用基本不等式得出a+
,4),利用基本不等式得出a+ 的最大值为-4,从而A中共含有最少个整数,求得此时实数a的值;②a=0时,-4(x-4)>0,解集为(-∞,4),整数解有无穷多,不符合条件; ③a>0时,[x-(a+
的最大值为-4,从而A中共含有最少个整数,求得此时实数a的值;②a=0时,-4(x-4)>0,解集为(-∞,4),整数解有无穷多,不符合条件; ③a>0时,[x-(a+ )](x-4)>0,此时整数解有无穷多,不符合条件.
)](x-4)>0,此时整数解有无穷多,不符合条件. )](x-4)<0,其中a+
)](x-4)<0,其中a+ <0,
<0, ,4),
,4), =-(-a-
=-(-a- )≤-2
)≤-2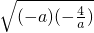 =-4,
=-4, ,即a=-2时取等号,
,即a=-2时取等号, 的最大值为-4,当且仅当a+
的最大值为-4,当且仅当a+ =-4时,A中共含有最少个整数,此时实数a的值为-2;
=-4时,A中共含有最少个整数,此时实数a的值为-2; )](x-4)>0,其中a+
)](x-4)>0,其中a+ ≥4,
≥4, ,+∞),整数解有无穷多,故a>0不符合条件;
,+∞),整数解有无穷多,故a>0不符合条件;

科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 选作题,本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
选作题,本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
|
| x2 |
| 12 |
| y2 |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com