
【题目】对于数列![]() ,称
,称![]() (其中
(其中![]() )为数列
)为数列![]() 的前k项“波动均值”.若对任意的
的前k项“波动均值”.若对任意的![]() ,都有
,都有![]() ,则称数列
,则称数列![]() 为“趋稳数列”.
为“趋稳数列”.
(1)若数列1,![]() ,2为“趋稳数列”,求
,2为“趋稳数列”,求![]() 的取值范围;
的取值范围;
(2)若各项均为正数的等比数列![]() 的公比
的公比![]() ,求证:
,求证:![]() 是“趋稳数列”;
是“趋稳数列”;
(3)已知数列![]() 的首项为1,各项均为整数,前
的首项为1,各项均为整数,前![]() 项的和为
项的和为![]() . 且对任意
. 且对任意![]() ,都有
,都有![]() , 试计算:
, 试计算:![]() (
(![]() ).
).
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面为正方形,△PAD为等边三角形,平面PAD丄平面PCD.
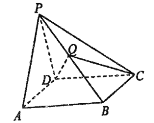
(1)证明:平面PAD丄平面ABCD:
(2)若AB=2,Q为线段的中点,求三棱锥Q-PCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新中国昂首阔步地走进2019年,迎来了她70岁华诞.某平台组织了“伟大的复兴之路一新中国70周年知识问答”活动,规则如下:共有30道单选题,每题4个选项中只有一个正确,每答对一题获得5颗红星,每答错一题反扣2颗红星;若放弃此题,则红星数无变化.答题所获得的红星可用来兑换神秘礼品,红星数越多奖品等级越高.小强参加该活动,其中有些题目会做,有些题目可以排除若干错误选项,其余的题目则完全不会.
(1)请问:对于完全不会的题目,小强应该随机从4个选项中选一个作答,还是选择放弃?(利用统计知识说明理由)
(2)若小强有12道题目会做,剩下的题目中,可以排除一个错误选项、可以排除两个错误选项和完全不会的题目的数量比是![]() .请问:小强在本次活动中可以获得最多红星数的期望是多少?
.请问:小强在本次活动中可以获得最多红星数的期望是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱柱ABCD-A1B1C1D1的底面为菱形,AA1⊥底面ABCD,∠BAD=120°,AB=2,E,F分别为CD,AA1的中点.
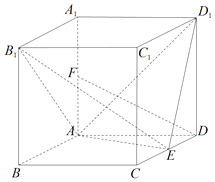
(Ⅰ)求证:DF∥平面B1AE;
(Ⅱ)若直线AD1与平面B1AE所成角的正弦值为![]() ,求AA1的长;
,求AA1的长;
(Ⅲ)在(Ⅱ)的条件下,求二面角B1-AE-D1的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了学生的健康,对课间操活动做了如下规定:课间操时间若有雾霾则停止课间操,若无雾霾则组织课间操.预报得知,在未来一周从周一到周五的课间操时间出现雾霾的概率是:前3天均为![]() ,后2天均为
,后2天均为![]() ,且每一天出现雾霾与否是相互独立的.
,且每一天出现雾霾与否是相互独立的.
(1)求未来5天至少一天停止课间操的概率;
(2)求未来5天组织课间操的天数X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面有5个命题:
①函数![]() 的最小正周期是
的最小正周期是![]() ;
;
②终边在![]() 轴上的角的集合是
轴上的角的集合是![]() ;
;
③在同一坐标系中,函数![]() 的图象和函数
的图象和函数![]() 的图象有3个公共点;
的图象有3个公共点;
④把函数![]() 的图象向右平移
的图象向右平移![]() 得到
得到![]() 的图象;
的图象;
⑤角![]() 为第一象限角的充要条件是
为第一象限角的充要条件是![]() .
.
其中,真命题的编号是______(写出所有真命题的编号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列叙述中正确的是( )
A.若a,b,c∈R,且a>c,则“ab2>cb2”
B.命题“对任意x∈R,有x2≥0”的否定是“存在x∈R,有x2≤0”
C.“![]() ”是“y=sin(2x+φ)为偶函数”的充要条件
”是“y=sin(2x+φ)为偶函数”的充要条件
D.![]() 是一条直线,α,β是两个不同的平面,若l⊥α,l⊥β,则α∥β
是一条直线,α,β是两个不同的平面,若l⊥α,l⊥β,则α∥β
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com