
【题目】已知![]() 为奇函数,
为奇函数,![]() 为偶函数,且
为偶函数,且![]() .
.
(Ⅰ)求函数![]() 及
及![]() 的解析式;
的解析式;
(Ⅱ)用函数单调性的定义证明:函数![]() 在
在![]() 上是减函数;
上是减函数;
(Ⅲ)若关于![]() 的方程
的方程![]() 有解,求实数
有解,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ,
,![]() (Ⅱ)详见解析(Ⅲ)
(Ⅱ)详见解析(Ⅲ)![]()
【解析】
试题(1)根据![]() ,
,![]() 的奇偶性便有
的奇偶性便有![]() ,联立
,联立![]() 便可解出
便可解出![]() 及
及![]() 的解析式;(2)根据减函数的定义,设任意的
的解析式;(2)根据减函数的定义,设任意的![]() ,且
,且![]() ,然后作差,可以得出
,然后作差,可以得出![]() ,根据对数函数的单调性便可得出
,根据对数函数的单调性便可得出![]() ,从而得出g(x)在(0,1)上单调递减;(3)求出
,从而得出g(x)在(0,1)上单调递减;(3)求出![]() ,根据
,根据![]() 便可得出
便可得出![]() 的范围,从而得出
的范围,从而得出![]() 的范围,根据对数函数的单调性便可得出
的范围,根据对数函数的单调性便可得出![]() 的范围,从而便可得出m的取值范围
的范围,从而便可得出m的取值范围
试题解析:(Ⅰ)∵![]() 为奇函数,
为奇函数,![]() 为偶函数,
为偶函数,
∴![]() .
.
又![]() ①
①
故![]() ,即
,即![]() ②
②
由①②得:![]()
![]()
![]() .
.
(Ⅱ)设任意的![]() ,且
,且![]() ,
,
则 ,
,
因为![]() ,所以
,所以![]()
![]()
所以![]() ,即
,即 ,所以
,所以 0
0
所以![]() ,即函数
,即函数![]() 在
在![]() 上是减函数
上是减函数
(Ⅲ)因为![]() ,所以
,所以![]() ,
,
设![]() ,则
,则![]()
因为![]() 的定义域为
的定义域为![]() ,所以
,所以![]() 的定义域为
的定义域为![]()
即![]() ,所以
,所以![]() , 则
, 则![]()
因为关于![]() 的方程
的方程![]() 有解,则
有解,则![]()
故![]() 的取值范围为
的取值范围为 ![]() .
.


 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,并且满足
,并且满足![]() ,
, ![]() .
.
(1)求数列![]() 通项公式;
通项公式;
(2)设![]() 为数列
为数列![]() 的前
的前![]() 项和,求证:
项和,求证: ![]() .
.
【答案】(1) ![]() (2)见解析
(2)见解析
【解析】试题分析:(1)根据题意得到![]() ,
, ![]() ,两式做差得到
,两式做差得到![]() ;(2)根据第一问得到
;(2)根据第一问得到![]() ,由错位相减法得到前n项和,进而可证和小于1.
,由错位相减法得到前n项和,进而可证和小于1.
解析:
(1)∵![]()
当![]() 时,
时, ![]()
当![]() 时,
时, ![]() ,即
,即![]()
∴数列![]() 时以
时以![]() 为首项,
为首项, ![]() 为公差的等差数列.
为公差的等差数列.
∴![]() .
.
(2)∵![]()
∴![]() ①
①
![]() ②
②
由①![]() ②得
②得
![]()
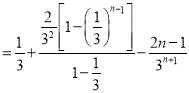
![]()
∴![]()
点睛:这个题目考查的是数列通项公式的求法及数列求和的常用方法;数列通项的求法中有常见的已知![]() 和
和![]() 的关系,求
的关系,求![]() 表达式,一般是写出
表达式,一般是写出![]() 做差得通项,但是这种方法需要检验n=1时通项公式是否适用;数列求和常用法有:错位相减,裂项求和,分组求和等.
做差得通项,但是这种方法需要检验n=1时通项公式是否适用;数列求和常用法有:错位相减,裂项求和,分组求和等.
【题型】解答题
【结束】
22
【题目】已知![]() ,
, ![]() 分别是椭圆
分别是椭圆![]() :
: ![]() (
(![]() )的左、右焦点,
)的左、右焦点, ![]() 是椭圆
是椭圆![]() 上的一点,且
上的一点,且![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() :
: ![]() 与椭圆
与椭圆![]() 交于不同两点
交于不同两点![]() ,
, ![]() ,椭圆
,椭圆![]() 上存在点
上存在点![]() ,使得以
,使得以![]() ,
, ![]() 为邻边的四边形
为邻边的四边形![]() 为平行四边形(
为平行四边形(![]() 为坐标原点).
为坐标原点).
(ⅰ)求实数![]() 与
与![]() 的关系;
的关系;
(ⅱ)证明:四边形![]() 的面积为定值.
的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知实数a、m满足a= ![]() cosxdx,(x+a+m)7=a0+a1(x+1)+a2(x+1)2+…+a7(x+1)7 , 且(a0+a2+a4+a6)2﹣(a1+a3+a5+a7)2=37 , 则m=( )
cosxdx,(x+a+m)7=a0+a1(x+1)+a2(x+1)2+…+a7(x+1)7 , 且(a0+a2+a4+a6)2﹣(a1+a3+a5+a7)2=37 , 则m=( )
A.﹣1或3
B.1或﹣3
C.1
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(1)求函数![]() 的最小正周期;
的最小正周期;
(2)若![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析:(1)根据二倍角公式和两角和差公式得到![]() ,进而得到周期;(2)由
,进而得到周期;(2)由![]() ,得到
,得到![]() ,
, ![]() ,由配凑角公式得到
,由配凑角公式得到![]() ,代入值得到函数值.
,代入值得到函数值.
解析:
(1)由题意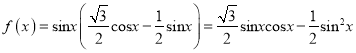
![]() =
=![]()
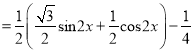
![]()
所以![]() 的最小正周期为
的最小正周期为![]() ;
;
(2)由![]()
![]()
又由![]() 得
得![]() ,所以
,所以![]()
故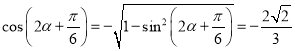 ,
,
故![]()
![]()
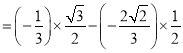
![]()
【题型】解答题
【结束】
20
【题目】为响应十九大报告提出的实施乡村振兴战略,某村庄投资![]() 万元建起了一座绿色农产品加工厂.经营中,第一年支出
万元建起了一座绿色农产品加工厂.经营中,第一年支出![]() 万元,以后每年的支出比上一年增加了
万元,以后每年的支出比上一年增加了![]() 万元,从第一年起每年农场品销售收入为
万元,从第一年起每年农场品销售收入为![]() 万元(前
万元(前![]() 年的纯利润综合=前
年的纯利润综合=前![]() 年的 总收入-前
年的 总收入-前![]() 年的总支出-投资额
年的总支出-投资额![]() 万元).
万元).
(1)该厂从第几年开始盈利?
(2)该厂第几年年平均纯利润达到最大?并求出年平均纯利润的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为 ![]() ,顶点A(a,0),B(0,b),中心O到直线AB的距离为
,顶点A(a,0),B(0,b),中心O到直线AB的距离为 ![]() .
.
(1)求椭圆C的方程;
(2)设椭圆C上一动点P满足: ![]() ,其中M,N是椭圆C上的点,直线OM与ON的斜率之积为﹣
,其中M,N是椭圆C上的点,直线OM与ON的斜率之积为﹣ ![]() ,若Q(λ,μ)为一动点,E1(﹣
,若Q(λ,μ)为一动点,E1(﹣ ![]() ,0),E2(
,0),E2( ![]() ,0)为两定点,求|QE1|+|QE2|的值.
,0)为两定点,求|QE1|+|QE2|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 上的点到它的两个焦的距离之和为
上的点到它的两个焦的距离之和为![]() ,以椭圆
,以椭圆![]() 的短轴为直径的圆
的短轴为直径的圆![]() 经过这两个焦点,点
经过这两个焦点,点![]() ,
, ![]() 分别是椭圆
分别是椭圆![]() 的左、右顶点.
的左、右顶点.
(![]() )求圆
)求圆![]() 和椭圆
和椭圆![]() 的方程.
的方程.
(![]() )已知
)已知![]() ,
, ![]() 分别是椭圆
分别是椭圆![]() 和圆
和圆![]() 上的动点(
上的动点(![]() ,
, ![]() 位于
位于![]() 轴两侧),且直线
轴两侧),且直线![]() 与
与![]() 轴平行,直线
轴平行,直线![]() ,
, ![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,
, ![]() .求证:
.求证: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设实数x,y满足不等式组  ,(2,1)是目标函数z=﹣ax+y取最大值的唯一最优解,则实数a的取值范围是( )
,(2,1)是目标函数z=﹣ax+y取最大值的唯一最优解,则实数a的取值范围是( )
A.(0,1)
B.(0,1]
C.(﹣∞,﹣2)
D.(﹣∞,﹣2]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=﹣1,|an﹣an﹣1|=2n﹣1(n∈N,n≥2),且{a2n﹣1}是递减数列,{a2n}是递增数列,则a2016= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com