
【题目】下列说法错误的是( )
A.若样本![]() 的平均数为5,标准差为1,则样本
的平均数为5,标准差为1,则样本![]() 的平均数为11,标准差为2
的平均数为11,标准差为2
B.身高和体重具有相关关系
C.现有高一学生30名,高二学生40名,高三学生30名,若按分层抽样从中抽取20名学生,则抽取高三学生6名
D.两个变量间的线性相关性越强,则相关系数的值越大
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 为函数
为函数![]() 的导函数.
的导函数.
(1)若![]() ,函数
,函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求a、
,求a、![]() 的值;
的值;
(2)若曲线![]() 上存在两条互相平行的切线,其倾斜角为锐角,求实数
上存在两条互相平行的切线,其倾斜角为锐角,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设无穷数列![]() 的前
的前![]() 项和为
项和为![]() ,已知
,已知![]() ,
,![]() .
.
(1)求![]() 的值;
的值;
(2)求数列![]() 的通项公式;
的通项公式;
(3)是否存在数列![]() 的一个无穷子数列
的一个无穷子数列![]() ,使
,使![]() 对一切
对一切![]() 均成立?若存在,请写出数列
均成立?若存在,请写出数列![]() 的所有通项公式;若不存在,请说明理由.
的所有通项公式;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ;数列
;数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
,![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)求数列![]() 的通项公式;
的通项公式;
(3)是否存在正整数![]() ,使得
,使得![]() 恰为数列
恰为数列![]() 中的一项?若存在,求满足要求的那几项;若不存在,说明理由.
中的一项?若存在,求满足要求的那几项;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 命题“x∈R,使得![]() ”的否定是:“x∈R,
”的否定是:“x∈R,![]() ”.
”.
B. “![]() 为真命题”是“
为真命题”是“![]() 为真命题”的必要不充分条件.
为真命题”的必要不充分条件.
C. ![]() ,“
,“![]() ”是“
”是“![]() ”的必要不充分条件.
”的必要不充分条件.
D. 命题p:“![]() ”,则﹁p是真命题.
”,则﹁p是真命题.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了提高职工的健身意识,鼓励大家加入健步运动,要求200名职工每天晚上9:30上传手机计步截图,对于步数超过10000的予以奖励.图1为甲乙两名职工在某一星期内的运动步数统计图,图2为根据这星期内某一天全体职工的运动步数做出的频率分布直方图.
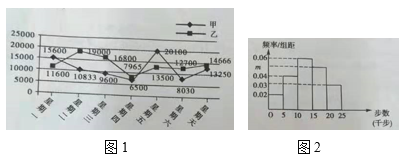
(1)在这一周内任选两天检查,求甲乙两人两天全部获奖的概率;
(2)请根据频率分布直方图,求出该天运动步数不少于15000的人数,并估计全体职工在该天的平均步数;
(3)如果当天甲的排名为第130名,乙的排名为第40名,试判断做出的是星期几的频率分布直方图.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个结论中正确的个数是
(1)对于命题![]() 使得
使得![]() ,则
,则![]() 都有
都有![]() ;
;
(2)已知![]() ,则
,则 ![]()
(3)已知回归直线的斜率的估计值是2,样本点的中心为(4,5),则回归直线方程为![]() ;
;
(4)“![]() ”是“
”是“![]() ”的充分不必要条件.
”的充分不必要条件.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在坐标原点
的中心在坐标原点![]() ,其焦点与双曲线
,其焦点与双曲线![]() 的焦点重合,且椭圆
的焦点重合,且椭圆![]() 的短轴的两个端点与其一个焦点构成正三角形.
的短轴的两个端点与其一个焦点构成正三角形.
(1)求椭圆![]() 的方程;
的方程;
(2)过双曲线![]() 的右顶点
的右顶点![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() .设
.设![]() ,当
,当![]() 为定值时,求
为定值时,求![]() 的值;
的值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() ,
, ![]() ,对于给定的非零实数
,对于给定的非零实数![]() ,总存在非零常数
,总存在非零常数![]() ,使得定义域
,使得定义域![]() 内的任意实数
内的任意实数![]() ,都有
,都有![]() 恒成立,此时
恒成立,此时![]() 为
为![]() 的类周期,函数
的类周期,函数![]() 是
是![]() 上的
上的![]() 级类周期函数.若函数
级类周期函数.若函数![]() 是定义在区间
是定义在区间![]() 内的2级类周期函数,且
内的2级类周期函数,且![]() ,当
,当![]() 时,
时, 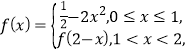 函数
函数![]() .若
.若![]() ,
, ![]() ,使
,使![]() 成立,则实数
成立,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com